 L’affaire est entendue : c’est la fin du monde dans quelques jours. Alors un grand merci à tous mes fidèles lecteurs qui m’auront suivi jusque là !
L’affaire est entendue : c’est la fin du monde dans quelques jours. Alors un grand merci à tous mes fidèles lecteurs qui m’auront suivi jusque là !
Et pour finir en beauté, nous allons bien sur parler de l’Apocalypse ! Mais comme il s’agit de sciences, nous allons discuter de la probabilité prochaine de la fin du monde.
Et vous allez voir que ça n’est pas si catastrophique que vous le pensez, mais c’est plus inquiétant que vous ne le croyez !
L’espèce humaine ne fait-elle que commencer ?
 Imaginons que vous arriviez dans votre bar préféré, et qu’un morceau soit en train de passer, par exemple The Scientist de Coldplay. La chanson fait environ 5 minutes, soit 300 secondes. Quelle est la probabilité que vous arriviez pendant les 15 premières secondes de la chanson ?
Imaginons que vous arriviez dans votre bar préféré, et qu’un morceau soit en train de passer, par exemple The Scientist de Coldplay. La chanson fait environ 5 minutes, soit 300 secondes. Quelle est la probabilité que vous arriviez pendant les 15 premières secondes de la chanson ?
Si on part du principe que vous arrivez au hasard pendant la chanson, il n’y a qu’une chance sur 20 que vous arriviez dans les 15 premières secondes; et donc 95% de chances que vous soyez dans les dernières 285 secondes. Tout cela est bien clair, mais vous vous demandez pourquoi je vous raconte ça ?
Tenons maintenant le même raisonnement avec l’espèce humaine plutôt qu’avec une chanson. L’espèce humaine a environ 50 000 ans, et selon le même principe, il y a 95% de chances qu’on ait déjà dépassé le premier vingtième de son existence. Donc il reste très certainement à l’espèce humaine moins d’un million d’années à vivre.
Ca ne vous fait pas paniquer ? Alors on va raffiner un peu. Mais pour cela, nous allons commencer par faire un détour par un problème d’espionnage.
Le problème des chars allemands
 Pendant la Deuxième guerre mondiale, les Alliés se sont posés la question cruciale de l’estimation du nombre de chars allemands en circulation. Les mathématiciens de l’Intelligence Service ont alors eu recours à une simple méthode probabiliste qui a surpassé toutes les autres approches.
Pendant la Deuxième guerre mondiale, les Alliés se sont posés la question cruciale de l’estimation du nombre de chars allemands en circulation. Les mathématiciens de l’Intelligence Service ont alors eu recours à une simple méthode probabiliste qui a surpassé toutes les autres approches.
Supposons que chaque char possède un numéro de série inscrit sur son blindage, et que ces numéros commencent à 1 et se suivent séquentiellement. Imaginez que vous soyez sur le champ de bataille, et que vous parveniez à détruire trois chars d’une division ennemie. En vous approchant de leurs carcasses, vous repérez les trois numéros de série : 17, 42 et 66. Combien y avait-il de chars au total dans cette division?
Intuitivement, on a envie de donner une réponse autour de 100. On sait en effet qu’il y en a au moins 66 (le plus grand numéro de série observé), mais s’il y en avait beaucoup plus, on serait très certainement tombés sur des numéros plus grands.
Poussons le jeu plus loin : imaginons que vous fassiez la même chose pour estimer le nombre de canons de l’adversaire, mais supposons que cette fois vous n’en capturiez qu’un seul ! Si son numéro de série est M, quelle estimation pouvez vous faire du nombre total de canons N ?
Il existe une réponse rigoureuse à cette question (voire plus bas pour les courageux), qui dit que la meilleure estimation est de doubler le numéro de série que l’on a obtenu. Intuitivement ça se comprend bien, si on choisit un seul numéro au hasard entre 1 et N, en moyenne on va tomber au milieu. Techniquement, on dit que si vous observez le numéro M et que vous cherchez à estimer le total N, le meilleur estimateur de N est de prendre le nombre 2M.
En développant un peu plus le calcul probabiliste, on peut même affirmer qu’à 95% de chances, N est inférieur à 20 fois le nombre M. Donc si vous avez observé le canon n°78, la meilleure estimation est 156, et à 95% de chances il y a moins de 1560 canons.
Ok pour les chars et les canons ? Alors revenons à nos moutons, ou plutôt nos humains.
L’argument du Doomsday
Savez-vous combien d’êtres humains ont vécu sur Terre depuis les débuts de l’espèce jusqu’à nos jours ? D’autres se sont posé la question, et un bon ordre de grandeur est environ 100 milliards. Ca veut donc dire que si les humains portaient tous un numéro de série séquentiel, le tien, cher lecteur, serait autour de 100 milliards (plus ou moins, suivant ton âge).
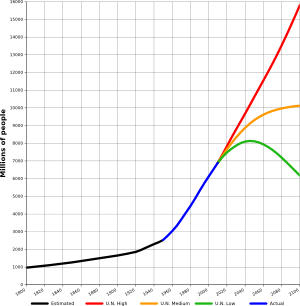 Vous me voyez venir : si je porte le numéro 100 milliards et que je ne suis qu’un humain quelconque parmi l’ensemble des humains passés, présents et à venir, alors je peux appliquer le même raisonnement que pour le char allemand. Et donc une bonne estimation de la taille totale de l’humanité jusqu’à son extinction est le double de mon numéro, soit 200 milliards d’individus; et à 95% de chances, pas plus que 2000 milliards.
Vous me voyez venir : si je porte le numéro 100 milliards et que je ne suis qu’un humain quelconque parmi l’ensemble des humains passés, présents et à venir, alors je peux appliquer le même raisonnement que pour le char allemand. Et donc une bonne estimation de la taille totale de l’humanité jusqu’à son extinction est le double de mon numéro, soit 200 milliards d’individus; et à 95% de chances, pas plus que 2000 milliards.
Partons du principe que la population mondiale va bientôt se stabiliser autour de 10 milliards (scénario orange ci-contre), avec un taux de natalité de 2%, soit 200 millions de nouveaux humains chaque année. Alors l’humanité en a encore en moyenne pour 1000 ans, et à 95% de chances pour moins de 10 000 ans. Et si on prend des projections pessimistes sur la croissance de la population (scénario en rouge ci-contre), ce sera encore pire ! Voilà ce qu’on appelle en anglais The Doomsday Argument.
Vous rigolez moins, là !
Tout cela est-il bien sérieux ?
Évidemment, en entendant ça on a juste envie de se dire un truc du genre « Oui mais non, on a pas le droit de faire des probas avec ce genre de choses » ou bien « Ca dépend de ce qu’on appelle l’espèce humaine ». Pour citer J.P. Delahaye dans son article sur le sujet [1] « Se rassurer à bon compte en s’interdisant de raisonner est trop facile. » Alors que peut-on vraiment conclure de ce raisonnement ?
Tout d’abord, il faut réaliser que tout cela part d’une vision assez copernicienne. Rappelez vous, Copernic avait provoqué un scandale en affirmant que la Terre n’était pas le centre de l’Univers, et que par conséquent la position de l’homme dans celui-ci n’avait absolument rien de spécial.
Eh bien là c’est pareil, admettons que vous n’avez rien de spécial et que je n’ai rien de spécial. Notre position dans l’espace n’a rien de spécial (ce que nous dit Copernic), mais notre position dans le temps non plus ! Si vous imaginez que la civilisation humaine va perdurer des millions d’années, coloniser la galaxie et que sa population va dépasser 100 000 milliards, alors vous êtes forcé d’admettre que le fait que vous soyez né parmi les premiers 100 milliards d’humains est un petit miracle. Si on considère que ce petit miracle est peu probable, alors il faut admettre que la population n’atteindra probablement jamais ces sommets.
Pour vous rassurer, on peut tenir le même raisonnement dans l’autre sens, pour affirmer que faire partie des derniers humains de l’espèce serait aussi un petit miracle. Donc n’ayez pas trop d’inquiétude pour cette semaine !
Pour aller plus loin : Fréquentistes versus Bayésiens
Quand j’ai découvert le problème du char allemand, cela a été une grande révélation pour moi, car j’ai enfin compris que la différence entre un fréquentiste et un bayésien n’est pas que philosophique.
Rappelons les termes du débat : en probabilités, un fréquentiste est quelqu’un qui pense que les probas n’ont de sens que si on les appliques à des problèmes pour lesquels on peut répéter une expérience des tas de fois, par exemple un lancer de dés. Un bayésien, c’est quelqu’un qui part de la formule de Bayes et utilise les probabilités pour désigner un niveau de croyance en une hypothèse, comme je l’expliquais dans mon billet sur l’inférence bayésienne. Le fréquentiste a une vision plutôt conservatrice de l’usage des probas, le bayésien prétend que l’on peut étendre leur usage à la quantification des niveaux de croyance. Et évidemment les deux chapelles se traitent mutuellement de tous les noms (dans les limites de la courtoisie scientifique !)
J’ai longtemps cru que cette différence était purement philosophique, car je ne voyais pas bien en quoi être fréquentiste ou bayésien pouvait changer les choses en pratique. Mais le problème du char allemand fournit un parfait exemple !
Le fréquentiste raisonne comme suit : supposons qu’il y a ait N chars et que j’en observe un seul qui porte le numéro M. J’essaye d’estimer le nombre total N à partir de la connaissance de M, sous la forme a.M où a est un nombre supérieur à 1. Je cherche le nombre a qui donne le meilleur estimateur.
Si je répète l’expérience un grand nombre de fois, je vais passer par les N cas possible : le premier cas est celui où j’observe le char n°1, le second cas celui où j’observe le char numéro 2, le ième cas est celui où j’observe le char numéro i. Si la forme que je cherche pour mon estimateur est de multiplier le numéro que j’observe par un nombre a, l’erreur moyenne que je commets est
\((1/N) \sum_{i=1..N} (ai – N)\)
et on observe que (pour les grands N) l’erreur moyenne devient nulle pour a=2. Donc pour un fréquentiste, on obtient un estimateur (dit non-biaisé) du nombre N de char en prenant le numéro observé et en le multipliant par 2.
Voyons comment procède le Bayésien. Lui part d’un certain niveau de croyance sur le nombre possible de chars ennemis. Par exemple supposons qu’on sache avec absolue certitude qu’il y en a moins que K, mais qu’entre 1 et K on ne privilégie aucune hypothèse. Notre probabilité a priori pour N (notée p(N)) est donc uniforme entre 1 et K. Maintenant ajoutons l’information : « J’observe le char numéro M ». Alors on obtient par la formule de Bayes une probabilité a posteriori p(N sachant M).
On peut faire le calcul en détail, je vous en fait grâce. Une fois qu’on a trouvé p(N sachant M), on peut calculer le N moyen en sommant sur tous les N possibles pondérés par cette probabilité. On trouve alors comme estimation moyenne de N
\(\frac{K-M}{log((K-1)/(M-1))}\)
C’est une valeur différente de ce qu’a dit le fréquentiste. Donc le fréquentiste et le bayésien vont clairement traiter différemment le problème du char allemand.
D’ailleurs pour ceux qui veulent encore pousser, il existe à l’origine une formulation bayésienne de l’argument de l’Apocalypse qui est due à Brandon Carter. Dans son article [1], J.-P. Delahaye semble résoudre le paradoxe en montrant qu’appliquer naïvement la formule de Bayes induit un effet de loupe qui fausse le résultat. Je me demande ce que devient cette réfutation si on prend le point de vue fréquentist (des avis ?).
Une bonne réponse est peut être justement qu’utiliser le raisonnement fréquentiste pour parler de la fin du monde est certainement la pire entorse qu’on puisse faire au fréquentisme, puisque la fin du monde est certainement l’expérience la moins répétable qui soit. Encore que, vu le nombre de fins du monde qu’on a déjà vécu….
[1] JP Delahaye, La Belle au bois dormant, la fin du monde et les extraterrestres, Pour la Science n°309


23 Comments
Sur le champ de bataille, la méthode probabiliste (ou bayésienne) suppose que les chars de la partie adverse aient un numéro de série entre 1 et le nombre total de chars présents. C’est irréaliste à deux titres: les chars d’en face sont des mélanges de plusieurs générations de chars ayant des numéros de série tirés quasiment au hasard parmi l’ensemble des chars produits. D’autre part, je ne connais pas d’industrie qui attribue un numéro de série à ses produit en commençant par 1, 2, 3 etc. Ne serait-ce que pour éviter de diffuser publiquement l’information du nombre de produits qu’elle a vendus 😉
Pour le calcul de la probabilité de fin du monde, l’hypothèse probabiliste suppose que la fin du monde est équiprobable quel que soit l’âge de l’humanité. Or sans être un millénariste new age, on peut légitimement penser que plus on a accumulé d’armes de destruction massive, plus la probabilité que notre monde vole en fumée est grande…
Oui pour les chars j’ai simplifié l’histoire. En fait je crois que les Alliés essayaient d’estimer la production mensuelle, et j’imagine que les chars devaient porter une indication avec le mois de production et un numéro. Je pense que même si les numéros ne commencent pas par 1 on doit pouvoir adapter le calcul (il faut alors un estimateur du numéro mini et du numéro maxi). Là où tu as raison, c’est que depuis c’est sur que plus personne ne donne des numéros de série simples (surtout pour les armes). Mais j’ai lu que quelqu’un avait adapté la méthode pour l’iPhone.
Je ne suis pas sûr que l’affirmation « l’hypothèse probabiliste suppose que la fin du monde est équiprobable quel que soit l’âge de l’humanité » soit juste. Dans la version fréquentiste, on raisonne sur la probabilité de vivre à une certaine époque étant donnée la longévité totale de l’humanité, mais on ne parle jamais de probabilité de la fin du monde étant donné un certain âge de l’humainté. Dans la version bayésienne, tu peux aller voir la formulation initiale de B. Carter qui prend justement en compte ce que tu dis, et le paradoxe existe quand même.
Pingback: The Doomsday argument : les mathématiques de la fin du monde | Dromologie | Scoop.it
Pingback: The Doomsday argument : les mathématiques de la fin du monde | Outbreaks of Futurity | Scoop.it
Le lien vers l’article de Delahaye est pourri… le bon est http://www2.lifl.fr/~delahaye/pls/107.pdf
J’avoue que j’ai un peu de peine à visualiser la différence fréquentiste/bayesien d’après les formules… Une petite interprétation numérique sur le cas des chars allemands m’aurait peut-être aidé…
Est-ce que le calcul selon lequel les météorites font 70 morts par an ( http://drgoulu.com/2012/01/28/risques-meteoritiques/ ) révèle si je suis fréquentiste (il me semble) ou bayésien (qui s’ignore ?) Et quel serait le calcul de l’autre tendance ?
Merci pour la correction du lien, c’est réparé !
Pour la différence fréquentiste/bayésien, il me faut peut être préciser le cadre d’application : je fais certaines observations d’un phénomène aléatoire, et j’essaye de tirer de ces observations de l’information sur la loi sous-jacente du phénomène. Le fréquentiste raisonne sur des « estimateurs », c’est à dire des formules permettant de reconstituer « de manière optimale » des caractéristiques du processus (comme sa moyenne, son écart-type, ou dans le cas du char la borne sup). Le bayésien suppose qu’il sait des choses sur la loi (probabilité a priori) et regarde en quoi les observations modifient ses croyances (en proba a posteriori).
Il me semble que dans ton cas des météorites tu n’es ni fréquentistes, ni bayésien, puisque tu ne cherches pas à reconstituer des caractéristiques du phénomène à partir des observations (à part peut être calculer la moyenne empirique et la prendre comme un estimateur de la moyenne « vraie », ce qui est effectivement plutôt fréquentiste je pense)
Pour un exemple numérique sur les chars, voir le paragraphe 8.9 de ce site qui est très bien http://greenteapress.com/thinkstats/html/thinkstats009.html. On y trouve par exemple le graphique explicite de la probabilité a posteriori étant donné une proba a priori (uniforme jusqu’à un « grand maximum ») et une observation d’un numéro.
Il y a généralement une confusion sur ce que sont les probabilités et leur sens pour l’individu : les probabilités ne s’appliquent pas à 1 individu. Dans le contexte de cet article, les probabilités permettent juste de dire que, pour une population de X individus choisis aléatoirement, on a a% d’individu qui font partie de premiers humains, b% qui font partie des derniers, que la majorité restante qui est entre les deux et que la précision de ces prévisions est proportionnelle à la taille de la population. Mais la probabilité ne nous permet pas de deviner la situation d’un seul individu.
Il existe une maladie génétique orpheline qui s’appelle la chorée d’Huntington. Elle est très rare. La probabilité d’avoir cette maladie pour chacun de mes arrières grands-parents était la même, très faible, pourtant l’un d’eux l’a eu. Mon grand père a-t-il hérité du gène délétère ? Le gène étant dominant, il avait une chance sur deux … il en a hérité. Mon père ? Aussi. mon petit-frère ? Aussi. Et moi ? En quoi les probabilités peuvent-elle répondre à cette question ? En rien. Les tests génétiques, si. Je ne l’ai pas.
Reblogged this on Et_voici_le_bb…des_mots! (&my_words_are): and commented:
Histoire de se calmer la caboche…
Pingback: The Doomsday argument : les mathématiques de la fin du monde | Acusmata | Scoop.it
Peux-tu imposer à l’estimateur fréquentiste la condition N < K, par analogie à l'exemple Bayésien, ce qui le rendrait plus comparable ?
Pour le débat fréquentistes/Bayésiens, voir les quelques tirs échangés il y a quelque temps dans les colonnes de La Recherche…
http://www.larecherche.fr/actualite/mathematiques/questions-a-nicolas-vayatis-bayesiens-contre-frequentistes-01-07-2008-75253
http://www.larecherche.fr/courrier/bayesiens-contre-frequentistes-faux-debat-01-11-2008-70381
http://www.larecherche.fr/courrier/bayesiens-contre-frequentistes-faux-debat-reponse-nicolas-01-11-2008-86699
Bonnes fêtes !
Sympa l’echange de tirs ! Bon pas tres profond non plus…
Pour imposer la condition N<K a l'approche frequentiste, je ne sais pas comment faire. Je pense que c'est justement contre-nature, dans le sens ou le frequentiste n'a aucun a priori. Une recherche Google sur "conditional estimation" renvoie des choses, mais la j'ai la flemme de lire !
Bonjour,
Bravo pour votre article que je trouves très intéressant et très bien écrit.
Je penses par contre que l’une de vos question est mal posée :
« Imaginons que vous arriviez dans votre bar préféré, et qu’un morceau soit en train de passer, par exemple The Scientist de Coldplay. La chanson fait environ 5 minutes, soit 300 secondes. Quelle est la probabilité que vous arriviez pendant les 15 premières secondes de la chanson ? »
La réponse à cette question n’est pas 1/20. Vous vous intéressez à une chanson en particulier parmi toutes les chansons qui passent dans la journée. Il y a donc, en plus du cas que vous arriviez pendant que la chanson en question soit diffuser, les cas de vous arrivez avant ou après que la chanson soit diffuser.
La question qui résume le mieux votre article serait quelque chose comme cela :
« Imaginons que vous arriviez dans un bar qui passe des morceaux de musique à la fil. Quelle est la probabilité que vous arriviez pendant le premier vingtième de la chanson actuellement diffusée? »
Bonne fête à vous !
Pour ma part je trouve que ce genre de petites entorses (volondaires, sans aucun doute) contribue grandement à la qualité de l’écriture, et au plaisir de la lecture. ça rend l’ensemble digeste et accessible même aux non-initiés ;-)… bon, j’ai quand même été largué vers la fin…
Très bien alors ! De toute façon, Mathieu, c’est ton jugement que je suivrai car je te considère comme mon lecteur « type » ! En tout cas le genre de lecteurs pour qui j’aspire à écrire. Donc le jour où tu trouves que je complique inutilement, il faut me le dire !
(Ah oui sinon pour résoudre le truc, il suffit de supposer que le bar passe toujours en boucle la même chanson toute la journée….)
Non tu ne compliques pas inutilement… Et quand tu le fais c’est toujours dans la partie « pour aller plus loin » donc le lecteur est prévenu!
Ceci dit pour en revenir au fond, je ne pense pas que les probabilités puissent s’appliquer ici. Entendons-nous bien, comme tu le sais je suis complètement hermetique aux mathématiques et donc absolument nul en probas (disons que je suis au scientifique ce que l’amateur d’art est au peintre 😉 mais il me semble que les probabilités n’ont de valeur « reelle » qu’à partir de notre position dans le temps.
Le present en tant que frontière entre le passé certain et le futur probable a un statut particulier au regard des probabilites. S’en extraire pour calculer des probas, puis s’y replonger pour en appliquer les conclusions, me semble quand même paradoxal… Mais bon, peut-être es-tu le Copernic du Temps et moi le tribunal religieux incrédule !
PS: meilleurs vœux à toi et toute ta famille!
Alors dans la famille Louapre, il y aurait au moins un scientifique et un ancien séminariste ?
BCBG tout ça et autant dire que la probabilité d’un telle configuration a bien baissé.
Bonne année !
Pingback: Podcast science 114 – Les hasards heureux
Trouvé un intéressant travail qui fait le lien entre le « doomsday argument » et « Le Grand Filtre » : Caitlin Grace, « Anthropic Reasoning in the Great Filter », 2010 [pdf]
Je suis moi aussi gêné par le côté statistique vs probabilité, que certains commentaires semblent évoquer.
Pour les chars allemands, on fait la supposition qu’ils ont été construits en un nombre fini, ou qu’ils sont encore en construction. On essaye de deviner leur nombre statistique, et on calcule la probabilité que ce nombre est plus ou moins correct.
Pour l’humain que je suis, affublé d’un numéro à 11 ou 12 chiffres, et qui regarde en arrière les 50 000 dernières années écoulées, je regarde précisément le numéro 500. Damned, si cet individu avait calculé la taille totale de l’humanité à venir, d’après son propre tirage il se serait planté d’un facteur 100 Millions en première approximation. Et avec 95% de probabilité que son monde ne voit pas plus de 20×500 de ses semblables, son erreur n’aurait été que d’un facteur 10 Millions, mais quand même. Est-ce à dire que nous sommes les survivants de ces 5% de probabilités ?
En poussant le raisonnement plus loin, et cette probabilité de 5% de 5% à appliquer tous les 10 000 individus, avec 100 Milliards / 10 Mille =10 Millions, je trouve 0,05^(10^7). Ceci est la probabilité qui a conduit l’humanité à me permettre de vivre ?
Bon, il doit y avoir un facteur exponentiel à prendre en compte, et je manque de formules pour cela, mais pour moi, plus l’événement se produit, plus il a de chances de se reproduire. C’est cela, être fréquentiste ?
Au-delà du catastrophisme et de notre application morbide à l’auto-destruction, ces chars allemands étaient récents, leur nombre forcément réduit, et la durée de vie de leur espèce plutôt courte (ils ont évolué, je vous l’accorde). Faut-il n’évaluer la survie à venir des humains qu’en termes de nombres d’individus, ou en nombre d’années ? Si, pendant la guerre, les alliés avaient vu un char pour la première fois en 1943, avec le numéro 77, ils auraient tout aussi bien pu se dire : ce char est un signe ! Nous en somme à la moitié de la guerre, et elle durera encore 4 ans ! (et à 95% de chance, elle durera encore moins de 40 ans ! ouf.)
Doubler le nombre d’individus, ou la durée de leur existence pour évaluer la fin de l’humanité ma parait aussi absurde que cette flèche qui n’atteint jamais la cible, puisque quand elle a parcouru la moitié de la distance, il lui reste encore une distance non nulle à parcourir.
Je suis assez de l’avis de JP Delahaye sur le fait que la formule de Bayes est à manipuler avec précaution et cela explique certaines choses.
Depuis son article il y a plus de 10 ans, d’autres personnes ont confirmé ses dires : un article dans la revue Tangente et une page Web sur le site du CNRS : http://images.math.cnrs.fr/L-Argument-de-l-Apocalypse-selon.html. Cette page est didactique et se limite à cerner les probabilités conditionnelles, mais elle n’aborde pas les aspects fréquentiels. Dans le cas de l’Apocalypse, ces travaux concluent à la « non-information » de différents tirages au sort, dont celui de l’Apocalypse. Tel que présenté par les différents auteurs, on ne peut rien conclure de plus, même si on connaît la formule de Bayes !
Cependant le problème des tanks allemands ne me semble pas aussi simple. Dans le cas de l’Apocalypse les humains seraient des boules non-numérotées sortant d’une urne : on a un simple numéro de sortie. Dans le cas des tanks, les boules ont chacune un numéro et chacune sort à un rang aléatoire.
Je pousse l’analyse plus loin.
1- Pour le premier problème, je sors une, puis deux, puis trois boules. Quelle est le nombre de boules dans l’urne ?
2 – Pour le second, on extrait la boule 125, puis 212, puis 157. Quelle est le nombre de boules dans cette seconde urne ?
La différence est plus que notable. Ainsi, on ne sait rien pour la première urne (ou si peu !). Par contre, on a une petite chance de faire une « bonne » approximation avec la seconde urne. Bayes ou fréquences… au pif : 400 boules. Mais au-delà, je préfère me taire.
Je vous invite à lire l’article du site du CNRS.
Pingback: Comment être sûr qu’un résultat scientifique est vrai ? | Science étonnante
Pingback: Les extraterrestres sont parmis nous ! (…c’est l’hypothèse la plus probable) | Science étonnante
Pingback: L'humanité aurait une chance sur 500 de disparaître avant la fin de l'année