C’est en cours de philo que j’en ai entendu parler pour la première fois ! Notre prof nous faisait un cours sur la logique et ses fondements, et c’est alors qu’elle le mentionna : le fameux théorème de Gödel, celui qui prouve que quoi qu’on fasse, il existe des énoncés mathématiques vrais, mais indémontrables. Les mathématiques resteront à tout jamais un édifice imparfait !
J’en fus évidemment tout retourné et fasciné : comment était-il possible qu’un truc pareil existe ? Comment prouver ce résultat pouvait même être du domaine de la science ?
Peut-on tout démontrer en mathématiques ?
Quand on fait des mathématiques, on manipule des énoncés. Un énoncé est une suite de symboles ou une phrase ayant un sens mathématique précis. Par exemple 2 + 2 = 4 ou "Il existe une infinité de nombres premiers" sont des énoncés mathématiques. Un énoncé mathématique est soit vrai, soit faux : par exemple 2 + 2 = 5 est un énoncé faux.
Quand on considère un énoncé mathématique, on ne sait pas forcément à l’avance s’il est vrai ou faux. Le travail du mathématicien, c’est justement d’essayer de savoir lesquels sont vrais et lesquels sont faux. Et pour cela, il utilise un outil : il fait des démonstrations.
Si un mathématicien arrive à démontrer un énoncé, on considère que cet énoncé est "vrai". S’il démontre le contraire, alors on dit que l’énoncé est faux.
Les mathématiques reposent donc sur l’idée que si un énoncé est vrai, alors il doit en exister une démonstration, et il n’y a plus qu’à la trouver. Mais est-on sûr que tout ce qui est "vrai" est forcément "démontrable" ? Se pourrait-il qu’il existe des choses vraies mais indémontrable ?
Notez bien que s’il existe des choses vraies mais indémontrables, c’est un camouflet pour les mathématiciens, car cela signifie qu’il y a des questions mathématiques auxquelles ils ne peuvent pas répondre ! Pour couper court à cette inquiétude, au début du XXème siècle, quelques matheux et logiciens menés par David Hilbert ont voulu asseoir les maths sur des bases inattaquables. Ils ont donc cherché à montrer que si une affirmation mathématique est vraie, alors il en existe nécessairement une démonstration.
Malheureusement pour eux, en 1931, le jeune logicien tchèque Kurt Gödel a douché leurs espoirs avec un résultat aussi diabolique qu’inattendu : en mathématique, il existera toujours des énoncés vrais, et pourtant indémontrables. Même sur leur propre terrain de jeu, les maths ne sont donc pas toutes puissantes !
Mais pour comprendre exactement de quoi il retourne, il nous faut creuser un peu la notion de « démontrable ».
A quoi jouent les mathématiciens ?
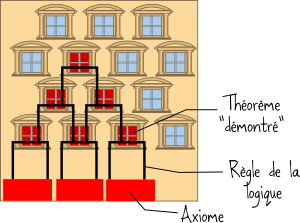Pour démontrer des choses, les matheux utilisent ce qu’on appelle la méthode axiomatique. Ils se donnent certaines affirmations comme ingrédients de départ : ce sont les axiomes. Puis ils cherchent à les combiner selon les règles de la logique pour essayer d’aboutir à de nouvelles affirmations. Une affirmation déduite des axiomes est considérée comme "démontrée" (on peut alors la qualifier de théorème).
Pour illustrer le principe de la méthode axiomatique, on peut utiliser une analogie avec un échafaudage. Les axiomes, ce sont les bases de notre échafaudage, et les règles de la logique nous permettent de monter une structure qui repose sur ces axiomes. Chaque fenêtre à laquelle on accède grâce à notre échafaudage est une affirmation démontrée qui devient un théorème.
Toutes les mathématiques se font au moyen de la méthode axiomatique, mais il existe plusieurs choix possibles pour les axiomes. Si vous voulez faire de la géométrie dans le plan, vous allez partir des axiomes d’Euclide. Si vous avez envie de considérer uniquement les nombres entiers, vous pouvez vous tourner vers les axiomes de l’arithmétique de Peano. Pour vous faire une idée de ce à quoi ça ressemble, voici quelques uns de ces axiomes :
- 0 est un nombre
- Tout nombre possède un suivant
- 0 n’est le suivant d’aucun nombre
- Si x=y et y=z, alors x=z
- etc.
Enfin si vous voulez faire des maths plus subtiles, vous devez utiliser un système d’axiomes plus travaillé. Aujourd’hui, LE système d’axiomes sur lequel reposent toutes les mathématiques modernes, c’est celui de la théorie des ensembles de Zermelo-Frenkel (noté ZFC pour les intimes). Ça veut dire que si de nos jours un mathématicien dit "J’ai démontré ceci", alors c’est sous-entendu "en utilisant les axiomes de ZFC".
Ce que dit le théorème de Gödel
Nous avons vu que la notion de "démontrabilité" est toujours relative à un système d’axiomes. Cela veut dire qu’une certaine affirmation mathématique peut très bien être démontrable avec un système, mais pas avec un autre ! Ce dont ont voulu s’assurer Hilbert et sa bande au début du XXème siècle, c’est qu’il était possible de construire un système d’axiomes parfait, tel que toutes les propositions mathématiques vraies y soient démontrables. Un tel système serait dit "complet".
Et c’est précisément cet espoir que Gödel a ruiné : il a démontré que dès que l’on veut faire au minimum de l’arithmétique des nombres entiers, quel que soit le système d’axiomes qu’on utilise, il existera toujours des énoncés vrais mais indémontrables. On dit que ces énoncés sont indécidables.
Cela signifie qu’il n’existe pas de système d’axiomes complet, et c’est pour cela que l’on appelle ce théorème, le théorème d’incomplétude.
Pour reprendre l’analogie avec l’échafaudage, on peut y mettre autant de piliers qu’on veut, il existera toujours des fenêtres de l’immeuble qu’on ne pourra pas atteindre !
Les implications pratiques du théorème de Gödel
En théorie, le théorème de Gödel est une catastrophe. Il nous dit que, aussi sophistiqués et nombreux que soient nos axiomes de départ, on va se retrouver avec des énoncés indécidables. Cela veut dire qu’il y a peut être des milliers de mathématiciens en train de passer leurs journées à chercher des démonstrations … de choses indémontrables !
Heureusement, en pratique, presque tout le monde se fiche du théorème de Gödel. En effet on s’est rendu compte que malgré tout, les propositions indécidables sont tellement tordues qu’on ne les croise pour ainsi dire jamais, et donc la quasi-totalité des propositions vraies « normales » sont démontrables avec les systèmes d’axiomes qu’on utilise. On est donc convaincus que l’on dispose de suffisamment de bon piliers à notre échafaudage pour atteindre toutes les fenêtres intéressantes.
Ainsi si aujourd’hui un mathématicien lambda cherche à faire une démonstration, sa principale crainte sera de ne pas être assez fort pour la trouver. Mais presque à aucun moment il n’envisage sérieusement que cette proposition soit « indémontrable ». Les conséquences pratiques du théorème de Gödel sont donc très limitées.
Une saveur de la démonstration
Je ne voudrais pas passer trop de temps à parler de la démonstration proprement dite. D’une part on la trouve décrite un peu partout d’autre part je trouve que c’est ce qui obscurcit souvent les présentations vulgarisées du théorème. Ceux qui ont mal à la tête peuvent arrêter là ! (N’oubliez pas que Gödel est mort fou, tout comme d’autres logiciens ayant traité des questions similaires comme Cantor, Zermelo, Post, Frege, Wittgenstein…enfin d’après Logicomix)
Pour démontrer son diabolique théorème, Gödel fait essentiellement une preuve « constructive » : il donne une recette pour fabriquer plus ou moins explicitement un énoncé arithmétique indécidable, et ce quel que soit le système d’axiomes de départ. Pour se faire une idée de ce dont il s’agit, Gödel mime en quelque sorte le paradoxe du menteur.
Vous connaissez certainement ce paradoxe, c’est celui d’un Crétois qui affirme « Tous les Crétois sont des menteurs ». Mais alors, lui-même dit-il la vérité à ce moment précis ? Une variante encore plus compacte de ce paradoxe, c’est l’énoncé « Cette phrase est fausse ». Alors, est-elle fausse…ou vraie ?
Le principe de la démonstration de Gödel, c’est de construire un énoncé qui dit « Je ne suis pas démontrable ». Vous voyez que si cet énoncé est vrai, alors…il n’est pas démontrable. Il est donc bien « indécidable » et le système d’axiomes est bien « incomplet ». En revanche si cet énoncé est faux, alors il est démontrable, et là c’est la catastrophe : on a un système d’axiomes qui démontre des choses fausses ! On dit que le système est inconsistant. D’ailleurs pour être précis, ce qu’a démontré Gödel, c’est qu’un système d’axiomes (contenant au moins l’arithmétique) est soit incomplet, soit inconsistant. Pas d’autre alternative.
Dans le détail, la démo repose sur une idée conceptuelle géniale, et sur une astuce diabolique.
L’idée conceptuelle géniale, c’est celle de la réflexion arithmétique des propositions méta-arithmétiques. Qu’est-ce que ça veut dire ? Si je dit « 2 + 2 = 4 », je fait un énoncé arithmétique. Si je dis « 2 + 2 = 4 est démontrable à partir des axiomes de Peano », je fais un énoncé « méta-arithmétique ». L’idée géniale de Gödel, c’est d’arriver à lier les deux. En gros il a montré que :
Pour tout énoncé E, il existe un autre énoncé S(E) tel que : E est démontrable si est seulement si S(E) est vrai.
Ce travail se fait au moyen d’une méthode de codage qui permet de transformer tout énoncé en un nombre entier et toute démonstration en une suite de nombres entiers. La démontrabilité de E se traduit donc comme une propriété arithmétique sur des suites de nombres, c’est l’énoncé S(E). Ensuite l’astuce diabolique, c’est ensuite de trouver UN énoncé particulier, noté G, tel que "S(G) = non-G". En appliquant le résultat précédent pour cet énoncé particulier G, on obtient alors l’affirmation
G est démontrable si est seulement si G est faux.
Donc soit G est vrai et il est donc indémontrable (et on a l’incomplétude), soit il est faux et démontrable (et on a l’inconsistance). Une fois de plus, si vous vous intéressez aux détails de cette démonstration, il faut creuser un peu plus et il y a plusieurs endroits où c’est décrit (par exemple ici).
Pour aller (vraiment) plus loin…
Pour ceux qui ont tenu jusque là et qui se posent quelques questions métaphysiques, voici quelques pistes de réflexion, sur des choses au sujet desquelles je ne suis moi même pas très à l’aise. Commentaires les bienvenus !
Pour commencer, il existe quand même quelques exemples de propositions indécidables et à peu près compréhensibles. Par exemple le théorème de Goodstein, qui concerne des simples suites de nombres (un peu comme la conjecture de Syracuse) : il est indécidable dans l’arithmétique de Peano, mais heureusement démontrable dans la théorie ZFC.
Un exemple plus sophistiqué, c’est le problème de Whitehead : c’est un énoncé de théorie des groupes pas trop difficile à comprendre (après le bac quand même), et pourtant indécidable même dans ZFC ! De même, un des exemples les plus connus est l’hypothèse du continu : existe-t-il un ensemble de nombres qui soit « plus grand » que N mais "plus petit" que R ? C’est indécidable !
Enfin, si on utilise la théorie des ensembles de Zermelo-Frenkel au sens strict (notée ZF), alors il existe un énoncé indécidable qu’on appelle l’axiome du choix. On choisit en général de l’ajouter à la liste des axiomes de ZF, pour obtenir la théorie ZFC.
Autre point pour ceux qui veulent creuser : Gödel a démontré un deuxième théorème d’incomplétude ! Le premier théorème dit que tout système est soit incomplet, soit inconsistant. L’incomplétude est un problème, mais l’inconsistance est une catastrophe ! On aimerait donc pouvoir s’assurer qu’un système donné est incomplet plutôt qu’inconsistant. Ce que dit le deuxième théorème, c’est qu’on ne peut pas démontrer la consistance d’un système formel en restant à l’intérieur de celui-ci.
Il y a quelque chose qui m’a longtemps troublé avec cette idée de propositions indécidables. Si on obtient une proposition vraie mais indécidable, alors on peut décider de l’ajouter comme axiome. Rien de bien troublant. Mais on peut aussi très bien décider d’ajouter son contraire à notre liste d’axiomes. Puisque la proposition est indécidable, on ne crée pas d’inconsistance. Mais qu’est-ce qu’on obtient si on fait ça ? Un système d’axiomes dont un axiome est une proposition "fausse". N’est-ce pas paradoxal ?
Pour résoudre la difficulté, il faut creuser la notion de "vrai". J’ai insisté sur le fait que la notion de « démontrable » était relative à un système d’axiomes. Par contre je suis passé vite sur la notion de « vrai », comme si elle était universelle et intrinsèque. En fait elle ne l’est pas, elle est relative à ce qu’on appelle un « modèle ». Pour l’arithmétique, il n’y a pas trop de débat sur quel est le modèle. Mais par exemple pour la géométrie, il y a plusieurs choix ! Le modèle classique est celui de la géométrie euclidienne. Pour trouver un système d’axiomes qui colle avec ce modèle, il faut prendre le 5ème axiome d’Euclide dans sa forme familière (une seule parallèle à une droite passe par un point donné). Mais si vous changez de modèle, par exemple la géométrie riemannienne, il vous faut un autre système d’axiomes qui va bien, et que l’on peut obtenir en modifiant le 5ème axiome (aucune parallèle ne passe par un point donné).
Donc si on choisit d’ajouter aux axiomes de Peano une proposition indécidable fausse, on obtient un système d’axiomes qui ne représente plus correctement l’arithmétique. Si j’ai bien compris, on peut considérer à la place des modèles d’arithmétique "non-standard", mais dont j’imagine que l’intérêt est limité (contrairement à la géométrie, où les modèles non-euclidiens ont un intérêt physique).
Mais pour les mathématiques de la théorie des ensemble, quel est le modèle raisonnable qui nous dit ce qui est vrai et ce qui est faux ? Une solution serait le modèle de l’Univers Constructible de Gödel, dans lequel l’axiome du choix (comme l’hypothèse du continu) sont "vrais" … mais je ne suis pas sûr de comprendre pourquoi !
Si vous êtes très malin, vous avez peut être eu l’idée de trouver un contre-exemple au théorème de Gödel et de construire un système d’axiomes parfait de la manière suivante : prendre toutes les propositions vraies, et les déclarer toutes « axiomes ». Même si ça n’est pas très intéressant en pratique, ça semble échapper à Gödel. La raison en est que Gödel suppose un système d’axiomes « récursivement énumérable » récursif. Cela signifie que les axiomes ont le droit d’être en nombre infini, mais il doit exister une procédure « finie » pour décider si une proposition donnée fait partie des axiomes ou non. Un système d’axiomes qui ne soit pas récursif n’a aucun intérêt pratique, puisqu’on ne peut jamais vérifier en temps fini si quelque chose est un axiome !
Enfin dernier point, les conséquences informatiques du théorème de Gödel sont souvent discutées (voire on trouve parfois le théorème énoncé sous cette forme) : la première conséquence, c’est qu’il n’existe pas de programme qui puisse dire si une proposition donnée est un théorème ou non. Une autre conséquence reliée, c’est qu’il n’existe pas de programme qui puisse dire avec certitude si un autre programme va terminer en temps fini, ou non (voir ici).
Bon j’ai largement dépassé 2000 mots, j’arrête. Vous pouvez reprendre vos activités normales !
[...] Le théorème d’incomplétude de Gödel [...]
pourrait on appliquer ce théorème à une autre science tel que la biologie?
C’est un des trucs que je n’ai pas mentionné : on fait souvent dire tout et n’importe quoi au théorème de Gödel, en essayant de l’appliquer là où il n’y a pas lieu.
"on ne sera jamais sur de rien" (gödelite aigüe) est assez dans la tendance "tout est relatif" (einsteinite aigüe)
Donc la réponse est : non
Le théorème de Gödel s’applique uniquement dans un cadre très precis : les systèmes formels basés sur un système d’axiomes récursivement énumerables contenant l’arithmetique.
Aviez – vous lu Godël Escher Bach de Douglas Hofstader ?
Il fait des parallèles intéressants entre le théorème de Godël, la musique de Bach et l’oeuvre d’Escher.
C’est un livre assez ardu mais magnifique et fascinant !
Pourquoi Bach ? Par la construction de sa musique parfois en canon qui fait référence à elle même.
Idem pour Escher avec des dessins s’auto référençant ou pas et plaçant le spectateur dans et/ou hors de l’oeuvre.
Il y a aussi pas mal de référence à l’informatique dans ses aspects les plus fondamentaux.
C’est bien écrit avec souvent les récits d’Achille et de la Tortue qui discourent sur la vérité ou pas de certaines idées tout en finesse !
Ce livre est un essai de vulgarisation sur le théorème de Gödel.
Douglas Hofstadter a d’ailleurs eu le prix Poulidser en son temps pour cet essai.
Oui je l’ai lu il y a quelques années, sans parvenir à le finir. Je l’ai reparcouru rapidement en écrivant ce billet, mais j’ai été un peu deçu. Je trouve qu’il plonge trop vite dans les concepts trop formels. Comme le livre est très long, je trouve qu’il aurait pu prendre son temps !
Bonjour, et merci pour cette article très intéressant (vraiment).
Je ne suis pas certain d’avoir tout bien compris dans els détails, mais j’ai à peu près compris l’idée
Par contre, en lisant ceci :
"Le premier théorème dit que tout système est soit incomplet, soit inconsistant. L’incomplétude est un problème, mais l’inconsistance est une catastrophe ! On aimerait donc pouvoir s’assurer qu’un système donné est incomplet plutôt qu’inconsistant. Ce que dit le deuxième théorème, c’est qu’on ne peut pas démontrer la consistance d’un système formel en restant à l’intérieur de celui-ci."
je me pose la question suivante :
On veut démontrer la consistance d’un système A. Si je comprends bien, pour cela il faut travailler dans un système B. Mais dans ce cas, la démonstration qu’on essaie de faire (que le système A est consistent) peut être inconsistente, et prouver que le système A est consistent alors que ce n’est pas le cas ?
Merci pour cette belle vulgarisation du théorème de Gödel ! Je signale juste une petite ambiguité : l’ensemble des axiomes doit être récursif, et non récursivement énumérable. En effet, comme c’est dit dans l’article, "il doit exister une procédure « finie » pour décider si une proposition donnée fait partie des axiomes ou non". Du coup c’est en fait l’ensemble des théorèmes qui sera récursivement énumérable : si un énoncé est un théorème, on finira toujours par le découvrir avec un peu de patience (en essayant toutes les preuves possibles à partir des axiomes). C’est pour les non-théorèmes qu’on est embêté !
En quoi "Tous les Crétois sont des menteurs" est il un paradoxe? Il signifie que le crétois qui le dit est un menteur, et qu’il existe donc des crétois qui disent la vérité.
Dans le langage courant un menteur est quelqu’un qui dit plus souvent que les autres – les gens "normaux" – le contraire de ce qu’il croit vai. Ce n’est donc pas quelqu’un qui dit toujours le contraire de la vérité, mais seulement quelqu’un qu’il est plus risqué de croire..
Les mathématiques utilisent les mots courants avec un sens précis, souvent tellement précis qu’avec le sens ordinaire des mots un énoncé mathématique n’a plus aucun intérêt.
A ma conaissance il n’y a pas de définition mathématique de "menteur"!
En fait ça l’est car cette phrase était énoncée par un Crétois…
"Mais on peut aussi très bien décider d’ajouter son contraire à notre liste d’axiomes. Puisque la proposition est indécidable, on ne crée pas d’inconsistance. Mais qu’est-ce qu’on obtient si on fait ça ?"
Je suis vraiment novice sur le sujet mais comme le remarque jch, autant la notion de "vrai" semble à peu près claire, autant son contraire (la "non-vérité") exprime un truc très vague: il peut exister un crétois qui dit la vérité, ou deux ou tous. Le "non-vrai" n’est pas vraiment une catégorie utile (de même que les "non-éléphants" ne sont pas une classification très utile en biologie) Du coup j’ai du mal à imaginer qu’on arrive à grand chose en ajoutant la négation d’une proposition dans une liste d’axiome…
Ce qui est amusant, c’est que si une théorie est complète alors il n’y a qu’un seul modèle.
Ce qui fait que si je peux construire deux modèles (non équivalent) alors la théorie incomplète.
Par contre le second théorème d’incomplétude dit surtout que la cohérence de la théorie n’est pas démontrable dans son propre langage.
En math c’est assez clair, une proposition est non-vraie (fausse) si son contraire est vrai. Donc c’est bien définit ! Il n’y a donc aucun problème à ajouter le contraire d’une proposition indécidable (contraire qui se trouve bien sûr elle-même tout aussi indécidable).
Pour visualiser, le mieux est de prendre la géométrie d’Euclide (qui rappelons le ne fait pas partie des systèmes formels "couverts" par Gödel, puisqu’il ne contient pas l’arithmétique) Si on ne prend que les 4 premiers axiomes (et pas celui sur les parallèles), on obtient un système incomplet puisque l’axiome des parallèle n’y est pas démontrable, ni son contraire. On peut décider de l’ajouter, mais on peut décider d’ajouter autre chose, comme le fait qu’il y a une ou une infinité de parallèles. Mais du coup on change de modèle.
Là où je rejoins ton point, c’est que stricto sensu, il faudrait décomposer l’axiomes des parallèles de la géométrie euclidienne en 2 axiomes :
5a) Il existe au moins une parallèle à une droite donnée passant par un point extérieur à cette droite
5b) Il existe au plus une parallèle etc.
Ni 5a ni 5b ne sont démontrables. Donc on peut décider d’ajouter non-5a (qui implique 5b) et on a zéro parallèle. Mais si on ajoute non-5b, ce que je me demande, c’est si on peut construire un modèle géométrique telle qu’il existe un nombre fini (disons 42) de parallèle à une droite donnée.
Mmh, en fait il vaudrait mieux écrire 5b sous forme d’unicité. Du genre si il existe D1 et D2 tel que (…) alors D1=D2. Mais je n’ai pas le courage de réfléchir à ce que veut dire la négation d’une proposition d’unicité…
Attention quand même, cela dépend de la nature de la proposition. Les formules non prouvables peuvent être vraies, ou indépendantes. Exemple :
1/
Pour toute théorie mathématique T, on peut (facilement, si si) construire un programme P (un algorithme) tel que la théorie ne pourra pas prouver que ce programme ne termine jamais.
Bien évidemment, ce programme ne termine pas, car s’il se terminait, on pourrait faire son execution pas à pas et cela constituerait une preuve qu’il s’arrête.
Donc même si "P s’arrête" et "P ne s’arrête pas" ne sont pas prouvable dans T, si j’ajoute l’un ou l’autre comme axiome, je vais avoir des problème : si j’ajoute celui qui est vrai, tout va bien, et T est un peu plus puissante. Si je rajoute celui qui est faux, je n’ai plus de modèle pour ma théorie, on peut donc considérer qu’elle n’est plus consistante, même si je n’obtiens pas de contradiction immédiate.
C’est le même problème avec la formule "la théorie T est consistante". Ce n’est pas prouvable dans T, mais on espère bien que c’est vrai ! et on ne va pas s’amuser à rajouter l’axiome contraire.
2/
Au contraire une formule F indépendante de T sera non prouvable dans T, et T+F ainsi que T + non F seront deux théories différentes valides comme l’exemple précédent sur les géométries qui seront euclidiennes, sphériques ou hyperboliques selon le nombre de parallèle à une droite par un point.
Tiens je ne suis pas sûr d’être d’accord !
Sur le point 1), je passe car je ne suis pas assez familier avec la formulation "algorithmique".
Sur le point 2), je n’arrive pas à comprendre ce que "indépendant" veut dire. Pour moi, une formule F est
d’une part :
- soit démontrable,
- soit réfutable,
- soit indécidable,
et ce caractère est relatif à la théorie T (c’est à dire au système axiomatique) considéré;
d’autre part :
- soit vraie
- soit fausse
et ce caractère est relatif au modèle M considéré.
Sachant qu’on peut très bien faire des maths en ne considérant qu’un système axiomatique T sans aucune référence à un modèle et ne jamais parler ni de "vrai" ni de "faux". Juste de ce qui est démontrable/réfutable et de ce qui ne l’est pas.
Donc pour moi, si on prend pour T les axiomes d’Euclide SANS le 5ème axiome (celui des parallèles), alors on a une proposition indécidable qui est le nombre de parallèles passant par un point donné. On peut choisir d’ajouter à T l’une des 3 versions du 5ème axiome : "une parallèle", "aucune parallèle", "une infinité de parallèles"
Maintenant si dans le même temps on a choisi de considérer comme modèle "la géométrie dans le plan", alors parmi les 3 versions du 5ème axiome, il n’y en a qu’une qui est compatible avec M ("vraie") et deux qui ne le sont pas. Donc si on fabrique T’ en ajoutant à T "aucune" ou "une infinité", alors T’ n’axiomatise plus M, mais un modèle M’ qui est Riemann ou Lobachevsky.
Ben je pense qu’on est d’accord. En tout cas ton explication me semble juste et compatible avec ce que j’ai dit avant.
Une proposition indépendante veut simplement dire qu’on peut étendre le modèle dans lequel on travaille par deux modèles différents, l’un ou la proposition est vraie et l’autre ou elle est fausse. Dans ce cas là, la proposition est forcément non prouvable.
Alors qu’une proposition peut être considérée comme vraie s’il n’existe pas de modèle dans laquelle elle est fausse. Dans ce cas là, on peut avoir une preuve de la proposition ou pas !
Sinon, je ne vois pas trop l’intérêt de faire des maths dans une théorie sans modèle. D’ailleurs en général, on fait toujours des maths dans un modèle, sans vraiment considérer la théorie qui est derrière. C’est le cas d’a peu près tous les maths classiques jusqu’en licence inclue (et même après). L’intérêt des maths est en général de comprendre les relations entre des objets d’un certain univers, on considère donc en général un univers avant une théorie.
Les seuls cas où on s’intéresse un peu à la théorie, c’est quand on utilise l’axiome du choix, mais en général, ça se transforme en voyage dans la quatrième dimension avec Zorn et compagnie. Et bien sur, quand on fait de la théorie des ensembles ou de la logique, on s’intéresse à ces questions.
Tous ces problèmes de non prouvabilité sont liés à des problèmes en physique. Le problème classique en mécanique est le problème à 3 corps. Tu considère un système à 3 corps liés par la gravitation et tu te demandes "est-ce qu’il va y avoir une collision ?". La réponse est indécidable. Bien sur, dans des cas simples, juste avant une collision, on pourra répondre "oui", ou "non pas d’ici 1 an". Mais si on cherche une réponse absolue, on ne peut pas toujours la donner. Pourtant soit il va y avoir une collision soit non, c’est donc une proposition non prouvable (ou non calculable), mais vraie ou fausse.
Au contraire, on peut faire des modèles d’univers bizarres (par exemple des multivers) tout à fait non prouvables qui peuvent être vrais (univers parallèles indépendants) ou faux (un seul univers). Mais s’il n’existe rien pour vérifier dans quel modèle on est, cela devient plus de la métaphysique.
J’espère avoir été plus clair !
En fait si une théorie est cohérente, il existe toujours un modèle de cette théorie ! (théorème de complétude de Gödel. Donc être indécidable est exactement équivalent à être vrai dans un modèle de la théorie et faux dans un autre.
@DK non, justement, je viens d’essayer d’expliquer que ce n’est pas équivalent, et qu’une proposition peut-être improuvable et vraie dans tous les modèles de cette théorie. Bon au temps pour moi pour ma pédagogie…
@Xoff : non j’avais bien compris ce que tu voulais dire, mais je pense que tu trompes.
En fait Gödel a aussi montré le théorème de complétude : si un énoncé est vrai dans tout modèle d’une théorie T, alors il est prouvable dans T.
cf cette page pour plus de renseignements : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_compl%C3%A9tude_de_G%C3%B6del
Hi hi, non ça n’a rien à voir. Il s’agit là des prédicat du premier ordre ! mais c’est beaucoup plus simple qu’une théorie mathématique classique. On ne peut pas faire de fonctions arithmétiques avec les prédicats du premier ordre et donc l’incomplétude ne s’applique pas à ce cas là. On ne parle donc pas de la même chose ici.
En gros, on a besoin de la multiplication et de la composition de fonction pour que les problèmes d’incomplétude apparaissent.
@Xoff: Le système de déduction utilisé est bien le calcul des prédicats, mais ça marche pour tout jeu d’axiomes ! Il ne faut pas confondre axiomes et règles de déduction. On peut par exemple prendre les axiomes de Peano (PA), qui sont suffisants pour le théorème d’incomplétude. La page wikipedia en anglais aide peut-être à y voir plus clair : http://en.wikipedia.org/wiki/G%C3%B6del's_completeness_theorem
En particulier la phrase suivante: "Precisely, we can systematically define a model of any consistent effective first-order theory T in PA".
Tu peux prendre n’importe quel système d’axiomes et te limiter à la logique du premier ordre et tout est décidable. Mais la plupart des formules intéressantes seront des formules de logique d’ordre supérieur !
D’où l’indécidabilité qui apparait. Mais oui, c’est vrai, si tu te limites à la logique du premier ordre, vrai = décidable. Mais tes formules ne décriront pas grand chose d’intéressant au niveau des structures de tes modèles. En particulier tu ne pourras pas faire de formules sur des propriétés véritablement arithmétiques dans le sens d’un calcul algorithmique.
Le théorème d’incomplétude concerne également la logique du premier ordre. Et on peut déjà dire des trucs très intéressants au premier ordre, comme la conjecture de Goldbach (tout entier pair à partir de 4 est la somme de deux premiers), ou la conjecture des nombres premiers jumeaux (il existe une infinité de nombres premiers jumeaux, c’est-à dire x et x+2 premiers).
Tu ne peux pas me dire d’abord que le théorème de complétude s’applique à tout pour ensuite me dire que le théorème d’incomplétude s’applique à tout
Il faut que tu choisisses (bien !)
En ce qui concerne la logique du premier ordre, le fait que la complétude existe ne veut pas dire que pour certaines formules on ait forcément déjà trouvé la preuve. Il y a une différence entre "une preuve existe" et "j’ai trouvé la preuve". Donc oui, il y a des formules de premier ordre intéressantes.
Comme le dit la page wikipédia que j’ai posté plus tôt : " The name for the incompleteness theorem refers to another meaning of complete".
Le théorème de complétude parle du système de déduction (ici le calcul des prédicats du premier ordre). Il affirme que si un énoncé est vrai dans tout modèle qui satisfait un ensemble d’axiomes A, alors on peut déduire cet énoncé depuis A, avec le calcul des prédicats. Par contre, il peut très bien rester des énoncés indépendants de cet ensemble d’axiomes.
Le théorème d’incomplétude dit justement que de tels énoncés existent, pour tout ensemble d’axiomes récursif contenant PA.
Donc ces deux théorèmes ne sont pas incompatibles et peuvent s’appliquer à une même théorie, malgré ce que leurs noms laissent entendre.
Je suis d’accord avec toi, mais je crois comprendre ce que tu n’as pas compris. Les énoncés du type Goldbach ne peuvent pas être indépendant : s’il est faux, il existe un contre-exemple qui sera un entier présent dans tous les modèles. Donc tu vois bien que ce type de proposition est soit prouvable soit vrai.
Pour avoir une proposition indépendante, il faut s’intéresser forcément à des propriétés plus complexes.
Indépendante ne veut pas dire non prouvable.
Dans le cas de Goldbach, effectivement il ne peut pas être faux (dans N !) et indépendant. Par contre il peut très bien être vrai dans N et indépendant. Cela tient au fait que c’est une formule très simple du type pour tout x blabla (où blabla ne dépend que de quelque chose de fini). On dit que la formule est de complexité Pi_1. Mais Goldbach pourrait très bien être un exemple de propriété indécidable, auquel cas elle serait forcément vraie dans N (et fausse dans un autre modèle).
Pour les nombres premier jumeaux par exemple ça se complique, car c’est une formule Pi_2, plus complexe, du type "pour tout x, il existe y, blabla". (pour tout x, il existe y>x, tels que y et y+2 sont premiers). Du coup, même si c’est toujours une formule du premier ordre, elle peut être vraie et indépendante, ou fausse et indépendante.
Bien sûr peut-être que ces deux formules sont démontrables et qu’on a juste pas trouvé la preuve, mais elle peuvent également être indémontrables.
Ah ben vous êtes chauds tous les deux !
Pour ma part, je crois avoir compris d’où vient mon erreur. Je pensais qu’un modèle associait nécessairement la valeur "vrai" ou "faux" à toute formule (syntaxiquement correcte) du langage choisit. Je ne pensais pas qu’un modèle pouvait être muet sur certaines formules. Mais il semble que si !
Non David tu avais bien raison, un modèle associe effectivement "vrai" ou "faux" à toute formule bien construite.
En fait pour moi, indépendant ça veut dire ni vrai ni faux ou plus raisonnablement vrai si on étends la théorie d’une certaine manière et faux si on le fait d’une autre manière.
Quand tu me dis "vrai dans N et indépendant" je ne comprends pas ce que tu veux dire.
@David oui, je crois que tu as compris ! Un modèle n’est qu’une collection d’objets "qui existent" et vérifient toute la théorie.
Tu peux relire le commentaire de ScienceEtonnnante plus tot, qui était très bien.
"démontrable et indécidable" sont des propriétés de la théorie.
"vrai et faux" sont des propriétés du modèle.
Il se trouve que si ton système de déduction est raisonnable, tu as
démontrable => vrai dans tout modèle
et si en plus ton système de déduction est complet (c’est le cas pour le calcul des prédicats utilisé habituellement), la réciproque est également vraie : vrai dans tout modèle=>démontrable.
Ce que j’entends par "vrai dans N et indémontrable" devrait être plus clair maintenant : dans N il n’y a pas de contre-exemple à la conjecture, mais il y en a dans des modèles "non-standards", qui comportent d’autres nombres entiers bizarres, et vérifient quand même les axiomes de Peano.
cette discussion devient marrante
mais je dois aller me coucher. Enfin pour moi un modèle n’est qu’une structure qui vérifie la théorie. Allez bonne nuit à tous.
Christophe, tu es un vrai physicien !
Voici ce que je crois avoir compris. Tout part d’un langage qui est un ensemble fini de symbole, à partir duquel on peut construire des chaînes finies de symboles (les formules), et des règles qui nous disent quels sont les formules syntaxiquement valides.
Bon, ensuite je crois comprendre qu’un modèle, c’est en gros "une application" qui à toute formule syntaxiquement correcte associe la valeur "vrai" ou "faux". Il y a certainement des contraintes à poser comme une sorte de "fermeture" ou "consistance" sous application des règles de la logique. Donc pour moi dans un modèle donné, toute formule correcte est soit vraie, soit fausse.
Si je te comprends bien Christophe, il y aurait une troisième possibilité qui est que le modèle ne dit rien sur certaines formules (que tu qualifies alors d’indépendantes). Dans une vision "à la physicienne", ça me va très bien comme situation (c’est à dire qu’un modèle est une représentation "réelle" ou "physique" d’un truc qui "existe"…- je mets des guillemets). Mais dans ma vision "formelle" (tout physicien que je sois) je pensais qu’un modèle se devait de se prononcer sur la véracité de toutes les formules du langages.
En l’espèce, il me semble que l’arithmétique dans N associe bien une valeur vrai ou faux à toute formule bien construite à partir des symboles usuels. Me trompe-je ? Se pourrait-il qu’il existe des formules arithmétiques indépendantes ?
Pour les axiomes, la situation est claire : on peut toujours ajouter un axiome qui est une formule indécidable, ou bien ajouter son contraire. Mais du coup on axiomatise plus l’arithmétique dans N, on axiomatise un autre modèle d’arithmétique non-standard.
Satané Gödel, je crois que je n’en comprendrai jamais vraiment tous les recoins !
Bon je vais me coucher aussi
Un modèle est juste une structure mathématique qui vérifie la théorie. Dans un modèle donné, chaque formule est vraie ou fausse, pas de troisième choix. Par exemple soit il existe une infinité de nombres premiers jumeaux dans N, soit non. Le problème c’est que la théorie décrit plusieurs modèles différents. C’est pour ça que certains énoncé sont indécidables : ils sont vrais dans certains modèles de la théorie et faux dans d’autres. Le théorème de Gödel dit que toute théorie parlant de l’arithmétique aura plusieurs modèles différents.
Après une bonne nuit de sommeil et en relisant nos postes, je suis d’accord avec DK. J’ai même raconté des âneries sur la logique du premier ordre parce que j’ai écrit trop vite et pensé au calcul sans quantificateurs !
Pour les modèles aussi, je suis d’accord, mais je réalise que j’ai une vue platonicienne des mathématiques. D’un point de vue métaphysique, je considère qu’un modèle existe ou pas. Cela n’empêche pas des modèles apparemment contradictoire d’exister en même temps, si on peut les mettre dans un modèle plus global (un peu comme différentes formes de géométries peuvent être considérées comme des cas particuliers dans une dimension supérieure si vous voyez ce que je veux dire).
Du coup je réalise que je n’ai rien compris à cette histoire de modèle non standard des entiers, car si on se limite aux "entiers finis" (un nombre fini de +1 après 0), tous les modèles représentent les mêmes entiers et je ne vois pas comment on peut être indépendant. Je vais aller voir un collègue logicien je pense.
La nuit porte conseil
Pour les entiers non standards, ce sont justement des entiers qui ne s’écrivent pas SSSS…SSS0. En fait même si c’est ce qu’on entend par "entier", aucun des axiomes de Peano ne force les entiers à être de cette forme, et c’est impossible de trouver des axiomes qui expriment ca.
Par exemple un modèle non standard de Peano peut ajouter aux entiers standards les entiers "non-standards" consistant en couples (x,y) où x est rationnel et y entier relatif. On peut définir l’addition et la multiplication sur cet ensemble bizarre, de manière a respecter les axiomes de Peano. Mais (2/3, -8) n’est pas de la forme SSS…SSS0.
[...] Le théorème d’incomplétude de Gödel [...]
Merci pour cette belle vulgarisation du théorème de Gödel ! Je signale juste une petite ambiguïté : l’ensemble des axiomes doit être récursif, et non récursivement énumérable. En effet, comme c’est dit dans l’article, « il doit exister une procédure « finie » pour décider si une proposition donnée fait partie des axiomes ou non ». Du coup c’est en fait l’ensemble des théorèmes qui sera récursivement énumérable : si un énoncé est un théorème, on finira toujours par le découvrir avec un peu de patience (en essayant toutes les preuves possibles à partir des axiomes). C’est pour les non-théorèmes qu’on est embêté !
Ah, merci de la correction !
[...] C’est en cours de philo que j’en ai entendu parler pour la première fois ! [...]
Il aurait été prétentieux de la part des mathématiciens de penser qu’ils peuvent construire un système parfait.
Les maths sont un langage, une construction, une interprétation, un description, bref tout ce qu’on veut sauf la réalité. Le "vrai" n"étant par ailleurs qu’une question de point de vue.
Je me suis toujours demandé également dans quelle mesure on pouvait décrire une réalité, ou ce qu’on en perçoit, quand on en fait partie.
Il parait donc évident (mais pas forcément facilement démontrable) que quoiqu’on fasse on rencontre des limites infranchissables.
Tiens ce commentaire montre que je n’ai pas bien fait mon travail !
Un des problèmes du théorème de Gödel est justement sa sur-interprétation dans un cadre plus large que celui qui est le sien. Je pensais avoir assez insisté là-dessus.
On entend parfois des réactions du genre "Ah les mathématiciens enfermés dans leur tour qui s’imaginent que tout est démontrable wouarf wouarf wouarf ! Et ils avaient besoin d’un théorème pour leur dire que non…" Or que ce soit clair à nouveau, le théorème de Gödel s’applique dans un cadre très restreint et très précis qui est celui des systèmes axiomatiques. Il n’y a aucune prétention à se demander si l’arithmétique est axiomatisable par un système complet.
Les matheux n’ont pas besoin de Gödel pour savoir que la proposition "Le Requiem de Mozart est-il beau ?" est indécidable…
D’ailleurs il existe des systèmes complets (comme l’arithmétique de Presburger, qui modélise les nombres entiers avec l’addition), ce qui démonte un peu les argumentations du type "Il aurait été prétentieux de la part des mathématiciens de penser qu’ils peuvent construire un système parfait."
Gödel se sent de plus en plus autrichien et surtout viennois : il aime la ville, son atmosphère intellectuelle et sa vie universitaire. Il demande, à la fin de l’été 1928, la nationalité autrichienne et n’est officiellement plus tchèque le 26 février 1929, trois jours après la mort de son père. Malgré son deuil, Gödel termine sa thèse de doctorat Sur la complétude du calcul logique qu’il présente le 6 juillet 1929 à son directeur de thèse Hans Hahn et à un de ses rapporteurs, Philipp Furtwängler. Dans ce mémoire dactylographié de 30 pages, le jeune mathématicien, âgé de 23 ans, expose divers résultats très importants de logique que nous allons détailler dans ce chapitre. Il démontre la complétude sémantique de la logique des prédicats du premier ordre, ce qui est satisfaisant pour l’esprit, et en déduit que tout système d’axiomes du premier ordre non contradictoire possède un modèle : il existe un ensemble d’objets qui vérifient les axiomes du système. Construire un modèle, c’est « ajouter de la chair autour des os » d’un système axiomatique, et ainsi établir qu’il est cohérent, c’est-à-dire non contradictoire.
wouaouw.. merci à Judith.D Ware, merci à cet illustre physicien, chercheur ,mais " ajouter de la chair autour des os" d un système axiomatique, établir qu il fut cohérent,non contradictoire,par un Mental sélectionné,ne signifie t il pas que cela nous dirige inévitablement vers La Source Centre Première?à vous Tous et toutes les Matheux "physiciens de la Matière", chercheurs de qualité et de savoir, le système, la recherche ne sera complète que lorsque la Conscience se marie avec la Science, pour une réunification Harmonieuse de tous
vos concepts établis, vos circuits mentaux élevés vers des Principes Spirituels conjugués.."Science sans conscience n est que ruine de L ame" de l homosapiens vers L homospiritus pour chacun , libre arbitre vers une Nouvelle Conscience Planéterre, actuellement dans l espace/temps 2013 sur Urantia( Notre Planète)!
Lire La Particule de Dieu- l ultimaton- l infinitron-le métatron-les muons- les huons-ect-Energie divine de la Créature vers le Créateur..Urantia BOOK- Brodcasturantia.com- destiné à toute l Humanité .CHERCHEURS DE L eSPRIT ! à bon lecteur Salut!
Bernadette de France!
Jacques Bouveresse dans "Prodiges et vertiges de l’analogie" s’est battu contre ceux qui disent n’importe quoi sur le théorème d’incomplétude, et notamment contre Regis Debray. Sur la vie de Gödel il y a le livre de Yannick Grannec "La Déesse des petites victoires", qui donne un bon aperçu de la "folie" de Gödel, de ses tourments intimes et de ses très bonnes relations avec Einstein.
Y a t-il un moyen de mesurer l’incomplétude, c’est à dire de savoir combien de fenêtres sont inateignables : 2 %, 50 % ?
Il faut lire le livre de Palle Yourgrau (Einstein/Gödel) qui explique notamment que pour Gödel le fait que l’on puisse trouver des solutions aux équations d’Einstein avec des courbes temps de genre fermé (univers de Gödel) démontre que la théorie de la Relativité Générale tombe sous le coup des théorèmes d’incomplétude. Selon lui, le temps de la RG n’est que le cour du temps. L’incomplétude en serait la flèche… C’est une idée que l’on ne souligne jamais quand on expose l’univers de Gödel.
En ce qui me concerne, je trouve toujours très spécieux d’insister sur la folie de Gödel… C’est souvent pour marginaliser ces résultats…
Pour ma part, j’énoncerais le théorème de Gödel ainsi :
"Toute théorie capable de formaliser l’arithmétique, si elle est récursivement axiomatisable, ne peut-être complète et consistante à la fois. La consistance d’une telle théorie est intrinsèquement indécidable"
Le second alinéa du théorème (que l’on nomme parfois second théorème d’incomplétude) dit que compléter trivialement les axiomes ne sert à rien : l’ensemble axiomatique peut-être fini ou infini dénombrable, le théorème de Gödel s’applique…
N’en déplaise à Jacques Bouveresse, une théorie qui se dispense de formaliser la structure logique de l’arithmétique (même dans le cadre des sciences humaines…) ou qui ne serait par récursivement axiomatisable n’est plus une théorie… C’est ainsi que par exemple, pour Gôdel, la relativité restreinte, n’accède pas au rang de théorie…
Les résultats de Gödel ne sont pas la propriété d’une élite (Sokhal et Bouveresse en font-ils partie ?). Il est plus aisé aujourd’hui pour un jeune lycéen qui baigne depuis toujours dans le monde de l’informatique de comprendre Godel ou le problème de l’arrêt de Turing…
Bouveresse reste peut-être aussi attaché au positivisme logique car finalement il n’a pas compris les résultats de Gödel…
J’ai trouvé que c’était de la très belle vulgarisation, mais quand même "les propositions indécidables sont tellement tordues qu’on ne les croise pour ainsi dire jamais" me semblent être assez déconnecté du sujet. Ne serait-ce que mentionner la possibilité de l’indécidabilité de P = NP me semble être complétement pertinent.