 Imaginons que vous soyez le chef de la diplomatie de votre pays, et que vos ambassadeurs aient besoin de vous envoyer des messages top secrets. Afin d’échapper aux oreilles de l’ennemi et de Wikileaks, vous allez avoir besoin de coder ces messages. Comment faire ?
Imaginons que vous soyez le chef de la diplomatie de votre pays, et que vos ambassadeurs aient besoin de vous envoyer des messages top secrets. Afin d’échapper aux oreilles de l’ennemi et de Wikileaks, vous allez avoir besoin de coder ces messages. Comment faire ?
La cryptographie basique
Pour cela, vous pouvez choisir une méthode simple, comme substituer une lettre par une autre dans l’alphabet. C’est le principe qu’utilisait César pour communiquer avec ses généraux. Les messages étaient codés de la manière suivante : chaque lettre est remplacée par la lettre située 3 cases plus loin dans l’alphabet : A devient D, B devient E, etc. En voici le principe en image pour coder le mot « BONJOUR » :
Les méthodes de substitution simples sont malheureusement assez peu sûres car chaque lettre est toujours codée de la même manière : on peut donc casser ces codes en faisant de la statistique et en analysant les occurrences des lettres : ainsi en français, le E est la lettre qui doit revenir le plus souvent, suivie des lettres AIST, qui bien sûr sont elles-mêmes bien plus fréquentes que WXYZ.
La cryptographie à clé
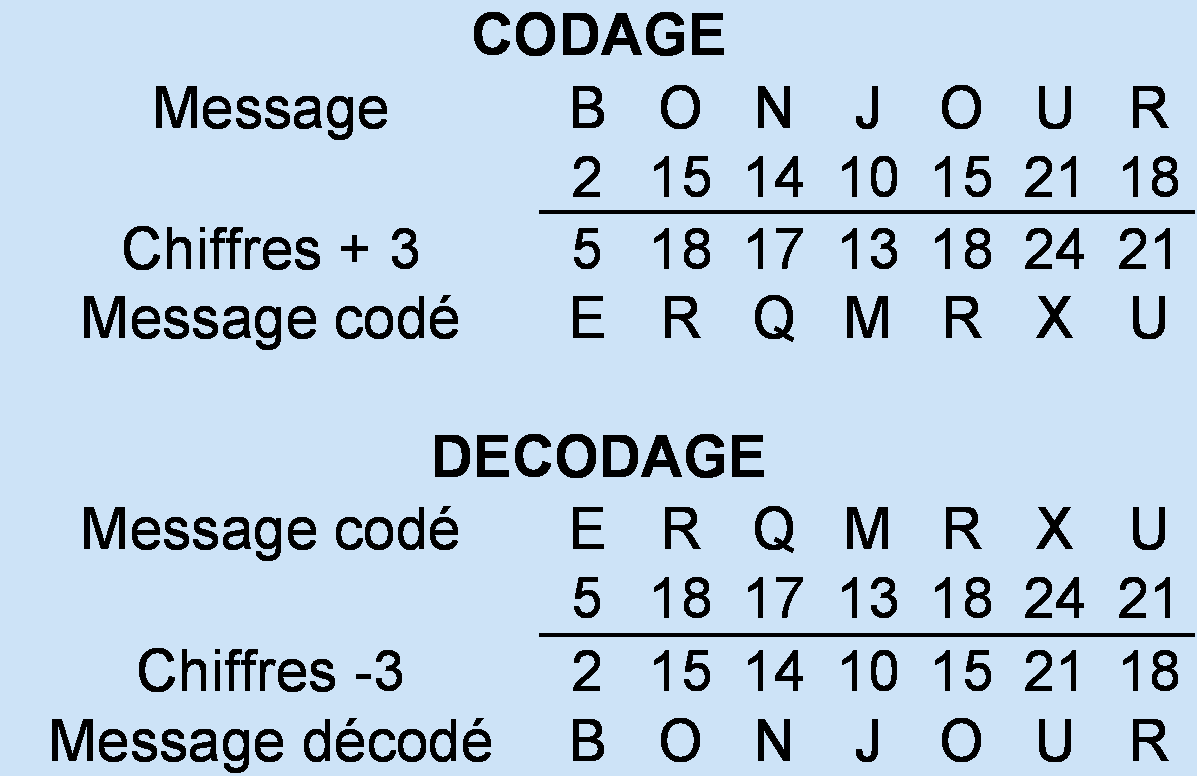
Pour éviter cela, il faut un codage dans lequel une même lettre n’est pas toujours codée de la même manière. C’est le principe des codes à clé. Imaginons que l’on veuille encoder le mot « BONJOUR » et qu’on choisisse comme clé de cryptage le mot « DECO ». On convertit chaque lettre du mot et de la clé en chiffre (A=1, B=2, …,Z=26), on les additionne et on reconvertit les chiffres obtenus en lettre. Comme la clé est souvent un simple mot, on la répète autant de fois que nécessaire pour coder l’ensemble du message. Pour décoder, on fait la même chose mais en soustrayant la clé au message codé. En voici l’illustration :
Et vous voyez ici que les deux lettres O du mot « BONJOUR » sont bien codées par une lettre différente. On ne peut pas facilement casser ce code par des analyses statistiques.
Toutefois le codage à clé pose un autre problème car il s’agit d’un codage symétrique : si vous savez coder les messages, alors vous savez aussi automatiquement les décoder. Donc si un espion parvient à se procurer la clé que vous donnerez à votre ambassadeur, alors l’ennemi saura ensuite décrypter les messages qu’il vous enverra !
La cryptographie asymétrique
La solution pour s’en sortir est d’utiliser une méthode de cryptographie asymétrique, c’est-à-dire où les procédures de codage et de décodage sont très différentes, de sorte que quelqu’un qui sache encoder les messages ne sache pas pour autant les décoder. Comment est-ce possible ?
Un algorithme asymétrique fait appel à deux clés : une clé dite « publique » qui sert à encoder le message, et une clé dite « privée » qui sert à le décoder. Donc si vous êtes le chef de la diplomatie, vous expédiez une clé publique à votre ambassadeur, et vous gardez pour vous la clé privée correspondante. Vos diplomates pourront encoder les messages, mais s’ils se font voler la clé publique, l’ennemi ne pourra pas pour autant décoder vos communications, car seule la clé privée permet de le faire !
L’algorithme RSA
L’algorithme asymétrique le plus populaire s’appelle l’algorithme RSA, en référence à ses concepteurs Rivest Shamir et Adleman (ci-dessous), qui l’ont inventé au MIT à la fin des années 70. Il est relativement simple car il ne fait appel qu’à des notions élémentaires d’arithmétique. Ceux qui veulent le calcul précis peuvent aller voir plus bas, mais pour ceux que les maths fatiguent, il est basé en gros sur le principe suivant : vous choisissez deux nombres premiers P et Q, vous les multipliez pour obtenir un nombre N=P.Q. Le nombre N donne la clé publique, alors que la privée nécessite de connaître la décomposition en P et Q.
Il est vrai qu’en théorie, la connaissance de la clé publique N permet de déduire la clé privée (P,Q) : il suffit de factoriser N. Sauf que factoriser un nombre peut être une opération très longue, même avec un gros ordinateur. Donc il suffit de choisir des nombres premiers suffisament grands et en pratique la décomposition de N en P*Q sera très difficile et le codage RSA impossible à violer par le calcul (sauf en un temps égal au nombre de protons dans l’Univers…)
Le RSA en pratique
L’algorithme RSA est assez difficile à utiliser pour chiffrer des grands messages, car bien que les opérations de base soient élémentaires (multiplication, puissance, division), les calculs peuvent se faire sur des nombres énormes et prendre pas mal de temps. Néanmoins pour des codes de carte bleue ou des requêtes vers des sites internet, ça reste faisable. D’ailleurs le RSA est largement employé dans ce type d’applications.
Pour en revenir à nos ambassadeurs, la puissance et l’importance stratégique du RSA est telle qu’en France, il a longtemps été classé « Arme de deuxième catérogie » (catégorie à laquelle appartiennent entre autres les Rafales, les porte-avions et les sous-marins). Dans le même genre, le gouvernement américain l’a aussi classé comme arme et a interdit pendant longtemps l’exportation de l’algorithme en dehors du territoire. Evidemment interdire l’exportation d’un algorithme, ça paraît difficile, et des petits malins anarcho-libertaires se sont amusés à se transformer en « arme d’exportation illégale » en se faisant tatouer l’algorithme RSA. Très tendance sur la plage…
Pour aller plus loin : le détail de l’algorithme RSA
Choisissez deux nombres premiers P et Q (que vous gardez pour vous), prenons par exemple P=5 et Q=11.
Fabriquez le produit des deux N=P.Q, dans notre cas N=55.
Choisissez un nombre E n’ayant pas de facteur premier commun avec (P-1).(Q-1) Dans notre cas puisque (P-1).(Q-1) = 40 = 2*2*2*5, on peut choisir par exemple E = 7.
La paire (E,N) constitue la clé publique, que vous donnez à votre ambassadeur
Choisissez ensuite un nombre D tel E.D mod (P-1).(Q-1) = 1 par exemple dans notre cas D = 23 fait l’affaire car 7*23 mod 40 = 1
La paire (D,N) constitue la clé privée, que surtout vous gardez pour vous.
Comment se passe la procédure d’encodage ? Tout d’abord il vous faut ramener votre message à un nombre. Vous pouvez le faire par le moyen que vous voulez comme A=01 ; B=02 ; … ;Z =26 par exemple. Une fois votre message traduit sous la forme d’un nombre M, vous allez encoder ce nombre avec la clé publique (E,N) de la manière suivante :
C = M^E modulo N
Pour décoder C (et donc retrouver M), il vous faut appliquer une opération différente, utilisant la clé privée (D,N) :
C^D modulo N.
Et c’est là que les maths des nombres premiers nous sont utiles, car elles permettent de prouver que ça marche c’est-à-dire que l’opération de décodage permet effectivement bien de retrouver le message M initial. On peut en effet démontrer que :
(M^E modulo N)^D modulo N = M
Crédits
- En tête : Matrix Core, Sourabh Rath, Flicker / CC
- Photo de Rivest, Shamir et Adleman, sur la page du labo de Leonard Adleman
- Photo de James Melvin et de son tatouage RSA





29 Comments
Bonjour,
Et si les nombres premiers avaient une fin.
Le dernier nombre premier aura comme carré un nombre qui sera divisible par un nombre plus petite que le dernier nombre premier.
exemple, si 5 est le dernier nombre premier, 5 au carré = 25;; 25 sera divisible par un nombre plus petit …que 5
dans ce cas cela ne marche pas, mais si on utilise le plus gros des supercalculateur mondiale. pourrais-t-on trouver une erreur dans la suite des nombres premiers et trouver la fin des nombres premiers.
SAUF SI JE SUIS, UN GÉNIE ET J’AI DÉCOUVERT LA FIN DES NOMBRES PREMIERS,?????????????????
merci, donnez-moi votre opinion SVP
Gérald Simard
30 rue Taché
Baie-Comeau, Qc
g4z 1v9
ge.simard@cgocable.ca
bonjour,
Supposons que l’ensemble des nombres premiers soit fini.
Soit a1, a2,….an l’ensemble fini des n nombres premiers.
le nombre « p=a1*a2*….*an +1 » est premier car si il existait « i » tel que ai divise p et ai différent de 1, alors comme ai divise a1*a2*….*an alors ai divise 1, ce qui n’est pas possible.
Or p est clairement supérieur à tous les n nombres premiers donc ne fait pas partie de n nombres premiers -> contradiction
Donc l’ensemble des nombres premiers n’est pas fini.
bonjour Géeald Simard,
Euclide a malheureusement déjà démontré, il y a bien longtemps, l’existence d’une infinité de nombres premiers 🙂
« Le dernier nombre premier aura comme carré un nombre qui sera divisible par un nombre plus petite que le dernier nombre premier. »
Soit P ce dernier nombre premier, donc son carré est P² dont les seuls diviseurs sont 1, P et P², puisque P est premier. Cela veut dire qu’il n’existe jamais de nombre diviseur plus petit que le dernier nombre premier… Par conséquent, l’hypothèse est réfutée.
Dans l’Antiquité, Euclide a démontré qu’il existe vraiment une infinité de nombres premiers.
Comment faire la steganographie par rapport à un Langage de programmation?
Pingback: Les nombres de Mersenne | Science étonnante
ce que je n’ai pas compris, c’est que dans toutes les manières si un espion vole la clé il pourra quand même décoder le message! Non?
Oui bien sûr ! Mais le gros avantage des systèmes de cryptage asymétrique (comme le RSA), c’est que la clé de codage (que doit posséder celui qui envoie le message) ne permet pas de décoder le message. Donc les risques de fuites de la clé de décodage sont beaucoup plus limités que dans un cryptage symétrique ou clé de codage et clé de décodage sont identiques !
sa dépend quelle clé il vole ,s’y il volent la clé a celui qui envoie des message , il ne pourra que crée est non decoder le message , dans le cas contraire ,s’y il volent la clé de celui qui li les messages il pourra alors les décodez ,mais la clé de décodage est celle que tu garde secrete est qui ne bouge jamais de ton coffre fort ,et na jamais été comuniqué
Merci pour la technique !!!! Bon bah maintenant je my colle pour faire comprdndre sa a mes amis 😀
RSA peut être encore renforcé parcequ’il a un ou deux défauts.
Le premier, c’est que pour une même clé et un même message en clair, il donnera un même message chiffré : C’est une faiblesse face aux attaques par replay.
Un attaquant peut s’amuser à chiffrer un certains nombre de messages connus en RSA et si il en trouve un qui est identique à ceux qu’il a espionné il sait que c’est le même message en clair.
Le deuxième, c’est que le chiffrement par clé RSA est beaucoup plus couteux en ressources machine qu’un chiffrement par clé symmétrique. Celà pose des problèmes quand on veut chiffrer du flux car la latence occasionnée par le chiffrement RSA rend le flux peu performant.
Heureusement, il y a un reméde.
Ce reméde est d’ailleurs implémenté dans les 2 grands protocoles de cryptographies que sont SSL/TLS et GPG.
On couple RSA avec un algorithme symmétrique (type AES par exemple). RSA chiffre la clé symmétrique pour qu’elle soit transmise sans encombres sur le canal puis le flux est chiffré avec cette clé symmétrique.
On peut encore renforcer la sécurité avec des signatures, des hashs et un protocole d’échanges de clés basé sur Diffie-Helman avec des courbes elliptiques.
Hum, faudrait peut-être que je fasse un article de blog là-dessus.
En attendant, voici un exemple d’implémentation. Le service que je vend : https://itis4u.ch/fr
Ou tu peux tout simplement ajouter une suite de quelques caractères aléatoires dans ton message.
Pingback: Chiffrement RSA et ordinateurs quantiques. | Portfolio Libersa Loïc élève en BTS SIO
Merci pour la vidéo et les explications autour du RSA, je comprends (enfin) comment fonctionnent les systèmes de codage avec clé publique/clé privée ! Tout est très clair et intéressant, comme d’habitude (https://www.youtube.com/watch?v=GME3fMeK5ts) ! 😉
Bonjour David,
tout d’abord merci pour tout votre travail pour la vulgarisation des sciences, très clairs et instructifs.
Pour cet article, je pense comprendre les mathématiques du raisonnement, j’ai écrit un petit script qui fait le travail et cela marche très bien. Néanmoins, une chose m’échappe.
Si l’attaquant connait N, alors il peut « facilement » trouver P et Q, car, de part la construction de N, la décomposition en nombres premiers est unique, donc il connait P et Q ? Dans ce cas, s’il connait aussi E (oui, il est malin, il a volé la clé publique en entier), alors il peut trouver un D qui permette de décoder le message.
Je suis conscient qu’il y a une erreur dans mon raisonnement, sinon cet algorithme n’aurait pas vraiment d’intérêt, mais je n’arrive pas à le voir. Pourriez vous m’éclairer.
Par avance merci
Benjamin
Bonjour,
Je me permets de répondre à la place de David.
Justement, pour des grands nombres, ce n’est pas « facile », cf le paragraphe plus haut dans l’article :
« Il est vrai qu’en théorie, la connaissance de la clé publique N permet de déduire la clé privée (P,Q) : il suffit de factoriser N. Sauf que factoriser un nombre peut être une opération très longue, même avec un gros ordinateur. Donc il suffit de choisir des nombres premiers suffisament grands et en pratique la décomposition de N en P*Q sera très difficile et le codage RSA impossible à violer par le calcul (sauf en un temps égal au nombre de protons dans l’Univers…) »
Bonjour,
effectivement je n’avais pas bien lu cette partie de l’article.
Merci pour votre réponse
Benjamin
bonjour,
En fait ce qui est implicite mais pas explicite c’est que les différentes opérations ne mettent pas du tout le même temps selon une conjecture non démontrée. Un modulo c’est rapide, ça revient à faire une division euclidienne, une opération de puissance c’est plus long mais ce qui est vraiment long c’est la factorisation en nombre premier.
Il y a une conjecture actuellement qui dit que pour décomposer un nombre en facteurs premiers, il faut essayer de le diviser par tous les nombres qui lui sont inférieurs et premiers, et si aucun ne marche il est premier. C’est la méthode par force brute, il n’existe pas de façon publique d’algorithme de factorisation rapide. On peut raffiner la force brute comme par exemple s’arrêter au nombre entier immédiatement supérieur à la racine carré du nombre à tester, ça va beaucoup plus vite mais fondamentalement on n’est pas dans du « rapide ».
Dans le cas présent, il existe des algorithmes qui permettent de générer sur la machine créant les clés des nombres premiers P et Q rapidement avec la garantie qu’ils soient premiers sans devoir tester si ils sont premier avec la méthode du paragraphe précédent. Mais pour la machine voulant cracker le code, décomposer P*Q « nécessite » la méthode par force brute.
La méthode par force brute est très très lente, car pour chaque nouveau nombre à tester, il faut le diviser par tous les nombres premiers inférieurs déjà obtenus, c’est à dire une liste de plus en plus longue. Par exemple, 4 est testé avec (2,3), 5 est testé avec (2,3), 6 est testé avec (2,3,5), 7 avec (2,3,5), 8 avec (2,3,5,7), 9 avec (2,3,5,7), 10 avec (2,3,5,7), 11 avec (2,3,5,7), 12 avec (2,3,5,7,11), 13 avec (2,3,5,7,11), 14 avec (2,3,5,7,11,13), 15 avec (2,3,5,7,11,13), 16 avec (2,3,5,7,11,13), 17 avec (2,3,5,7,11,13), 18 avec (2,3,5,7,11,13,17)….
On conjecture aussi que la proportion de nombres premiers dans un intervalle de N suffisamment grand est grosso modo constante. Donc le nombre d’opérations ne croit pas linéairement avec la taille du nombre dont il faut vérifier si il est premier.
Et régulièrement en créant cette liste pour la partie non enregistrée « en dur » dans le programme, on teste P*Q en le divisant par les nouveaux nombres ajoutés à la liste. Ce qui fait un nombre de calcul fabuleux si P et Q sont grands.
Mais bien sûr tout ceci repose sur la non existence d’un algorithme de factorisation rapide, ce qui n’a rien de certain. Même, on pourrait penser que les techniques d’espionnage « Yes we scan » systématiques de la NSA, organisme américain doté d’une tripotée de docteurs en mathématiques, sont une preuve suffisamment crédible du fait que cette conjecture soit fausse.
par proportion constante dans un intervalle, je voulais en fait dire ça, https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_nombres_premiers
Pingback: Benoît (benoittipe) | Pearltrees
Pingback: Les codes secrets — Science étonnante #10 – LightX
Bonjour à vous et un immense merci pour vos démonstrations.
Je suis informaticien, comme tout le monde, j’utilisais ces systèmes sans réellement en prendre conscience car nos ordinateurs utilise ce cryptage pour garantir tout messages à arriver à son destinataire sans pour autant que le monde entier reçoive celui-ci en même temps. (merci SSL, TLS,… etc)
Une question me viens, si c’est si long à décoder un RSA.. Comment la NSA, peut rapidement les décoder (en tenant compte de gens parano comme moi, crée des mots de passes dis « Fort ».
Vous démontrez la lenteur (mais pas l’irréalisable) dans le processus de décryptage sans connaissances des clés privées.
Comment font-ils alors pour aller si vite au décryptage svp?
La NSA ne peut pas décoder rapidement un message codé selon un chiffrement asymétrique. Ils doivent faire comme le commun des mortels : la méthode bourrin. Ils doivent tester tous les nombres premiers pour découvrir les deux facteurs de la clé public. Ça mets tellement de temps que ton codage est considéré inviolable.
Quand tu parles de mots de passe « forts » je pense aux mots de passe dont tu te sert pour créer un compte google ou te connecter sur Facebook. Sache que ces mots de passe n’ont aucune incidence sur le chiffrement des messages. Un mot de passe « fort » indique juste que si quelqu’un s’amuse à essayer d’accéder à ton compte en mode bourrin, il va galérer.
Pingback: Les codes secrets — Science étonnante #10 | JetBip
bonjour je suis en 4 eme et je n ai pas encore vu les nombre premier , mais pourquoi les machine quantique ne sont elles pas capable de factorisé un nombre plus grand que 143
Je prends un nombre plus grand que 143, je prends donc 147.
Or justement : 147 = 3 fois 7 fois 7, j’ai factorisé le nombre 147…
Les machines quantiques pour le calcul sont à leurs débuts, mais leurs progrès sont très prometteurs. Il est peut-être difficile de mettre en place une structure permettant la superposition quantique. Mais peu à peu on progresse.
Pingback: Générer des clés SSH modernes - tutox.fr
Salut.
Je suis actuellement en M2 de mathématiques fondamentales et pour mon UE de langue, en anglais, j’ai décidé de parler de cryptographie. Est-ce que tu aurais des références, simple, de vulgarisation, à propos de ça et de l’algorithme RSA ?
Merci d’avance.
Je ne sais plus très bien ce que j’avais utilisé comme réf à l’époque, mais l’article originel RSA est là
https://people.csail.mit.edu/rivest/Rsapaper.pdf
(mais ça n’est pas vulgarisé !)
Sinon il y a pas mal de références sur la page wiki
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
J’espère que ça aide 🙂