 Depuis l’avènement de la théorie des cordes, on entend souvent que nous vivrions en réalité dans un Univers à 10 dimensions. Mais cette affirmation est trompeuse, et ce indépendamment de la validité de ces théories. En effet le nombre de dimensions de l’espace-temps est une caractéristique du formalisme mathématique utilisé, et ne devrait pas être considéré comme une propriété physique mesurable de l’Univers.
Depuis l’avènement de la théorie des cordes, on entend souvent que nous vivrions en réalité dans un Univers à 10 dimensions. Mais cette affirmation est trompeuse, et ce indépendamment de la validité de ces théories. En effet le nombre de dimensions de l’espace-temps est une caractéristique du formalisme mathématique utilisé, et ne devrait pas être considéré comme une propriété physique mesurable de l’Univers.
La théorie des cordes
Un des problèmes fondamentaux de la physique théorique du XXIème siècle consiste en l’unification de la théorie de l’infiniment petit, la mécanique quantique, avec celle de l’infiniment grand, la relativité générale.
Cette tâche est extrêmement ardue tant sur la plan du formalisme mathématique qu’en raison des questions conceptuelles qui se posent. La théorie des cordes constitue à ce jour la tentative la plus développée pour réaliser cet exploit.
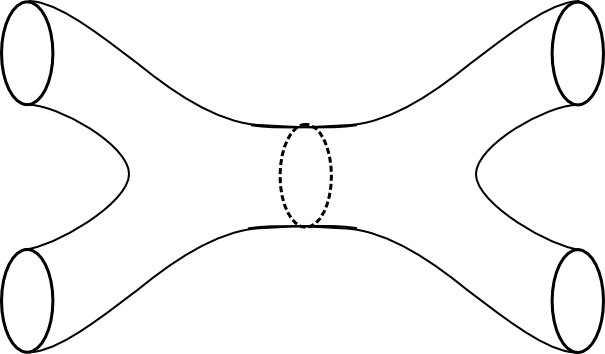 L’idée de base paraît assez claire : il s’agit en gros de refaire toute la physique quantique en partant du principe que les objets élémentaires ne sont plus des particules ponctuelles, mais de petites cordes ayant une certaine extension spatiale.
L’idée de base paraît assez claire : il s’agit en gros de refaire toute la physique quantique en partant du principe que les objets élémentaires ne sont plus des particules ponctuelles, mais de petites cordes ayant une certaine extension spatiale.
Ainsi au lieu d’avoir des particules qui interagissent pour en former d’autres, on aurait des petites cordes qui peuvent fusionner ou se diviser, ce que l’on peut représenter par de jolies structures bi-dimensionnelles comme celle-ci.
Et pourquoi 10 ou 26 dimensions ?
 Les traités de théorie des cordes commencent en général par exposer la théorie dite des cordes bosoniques. On formalise le postulat précédent de petites cordes qui interagissent, et on déroule le formalisme inspiré de la théorie quantique des champs.
Les traités de théorie des cordes commencent en général par exposer la théorie dite des cordes bosoniques. On formalise le postulat précédent de petites cordes qui interagissent, et on déroule le formalisme inspiré de la théorie quantique des champs.
Lire les premiers chapitres d’un bouquin de théorie des cordes est un moment ardu, mais d’une grande beauté formelle. L’idée de départ paraît géniale et tout s’enchaîne avec harmonie.
Malheureusement les ennuis commencent en général au chapitre 3, quand on décide vraiment d’introduire la mécanique quantique dans le bazar. Et là on se retrouve face à un gros problème qui porte le petit nom charmant d’anomalie conforme. Pour faire simple, le fait de passer à la version quantique de la théorie détruit certaines propriétés de symétrie qu’elle possédait au départ.
Pour une théorie quantique, l’existence d’une anomalie est en général considérée comme une maladie grave et l’histoire a bien failli s’arrêter là pour la théorie des cordes. Oui mais non, car il existe une échappatoire ! Ce que l’on appelle l’annulation de l’anomalie !
Pour vous faire une idée de ce qu’est l’annulation de l’anomalie, vous pouvez regarder l’équation ci-dessous, extraite d’un des articles fondateurs [1]. Comme l’indiquent les auteurs, l’anomalie qui nous embête tant se traduit par le fait que le membre de droite n’est pas nul.
Vous ne comprenez rien à l’équation ? Peu importe, regardez bien ! Si je pose D=26 (et alpha0=1), le membre de droite s’annule, l’anomalie disparaît et notre théorie est sauvée ! Eh bien qu’à cela ne tienne, posons D=26 et continuons de développer la théorie !
La dimension critique D=26 concerne la théorie des cordes dite « bosoniques», qui pour d’autres raisons a depuis été remplacée par la théorie dite « supersymétrique ». La théorie supersymétrique possède également une anomalie conforme, mais pour elle aussi le miracle se produit : l’anomalie s’annule, mais cette fois-ci en 10 dimensions.
 Alors que faire de mes 10 dimensions ?
Alors que faire de mes 10 dimensions ?
La suite de l’histoire est assez connue : puisque la théorie des cordes ne peut exister qu’en 10 dimensions, il faut trouver un moyen de s’accommoder des 6 dimensions supplémentaires. La solution consiste à les replier sur elles-mêmes, un peu comme quand on roule une feuille de papier très finement. Les espaces de dimensions 6 qui vont bien s’appellent les espaces de Calabi-Yau (la figure ci-contre en montre une projection, j’espère que ça vous donne envie de vous y promener !)
Ce qui se déroule dans ces 6 dimensions ne nous est pas directement accessible, mais se manifeste dans les quantités physiques (comme des probabilités de transition) que l’on peut calculer, et qui dépendent de la géométrie de l’espace de Calabi-Yau choisi.
10 dimensions, une prédiction physique ?
Une première remarque s’impose : contrairement à ce qu’on peut lire, l’existence de 6 dimensions supplémentaires n’est pas vraiment une prédiction de la théorie des cordes, il s’agit plutôt d’une condition mathématique pour que la théorie existe.
Ensuite, la notion de dimension est un concept délicat : il ne s’agit pas en effet d’une propriété physique, mesurable directement par une expérience, mais plutôt d’une propriété du formalisme mathématique utilisé. La théorie des cordes est formulée dans des espaces topologiques de dimension 10.
En physique classique, la différence peut paraître insignifiante entre propriété physique et propriété du formalisme mathématique. Ceci est dû au fait qu’en général quand on introduit un objet mathématique (par exemple un champ de température), celui-ci correspond à une quantité physique mesurable, au moins en principe.
Toutefois avec l’avènement de la mécanique quantique et de la relativité générale (et dans une moindre mesure en électromagnétisme), la différence entre objets mathématiques et quantités physiques mesurables tend à s’accentuer : tous les objets mathématiques que l’on introduit pour développer ces théories ne sont pas nécessairement mesurables. Par exemple on ne peut pas directement mesurer une fonction d’onde ou une métrique d’espace-temps.
Une des conséquences est qu’en physique quantique, on peut imaginer deux théories utilisant des objets mathématiques différents, mais dont les prédictions physiques mesurables soient strictement identiques ! (pour les curieux, vous pouvez penser à la formulation en intégrale de chemin de la mécanique quantique, ou bien à la formulation de Palatini de la relativité générale)
Des dimensions supplémentaires ? Pas de quoi en faire tout un plat…
Dans le cas de la théorie des cordes, les 6 dimensions supplémentaires appartiennent à la catégorie des objets mathématiques non-directement mesurables. La géométrie de l’espace de Calabi-Yau influe sur le calcul des quantités physiques mesurables, mais ces dernières seront in fine présentées en 4 dimensions.
Une autre manière de le dire : on peut parfaitement imaginer qu’il existe une théorie formulée uniquement en 4 dimensions, et dont les prédictions physiques soient identiques à celles de la théorie des cordes.
Donc affirmer que l’Univers (avec un grand U) possède 10 dimensions, n’a pas grand sens car ça n’est pas une affirmation sur la physique de celui-ci. Mais bon, reconnaissons-le, les dimensions supplémentaires ça aide à faire rêver les gens avec de la physique théorique, et ce noble but mérite bien quelques entorses !
[1] Un des textes fondateurs : Goddard et al., Quantum Dynamics of a Massless Relativistic String, Nuclear Physics B 56, 109-135 (1973)
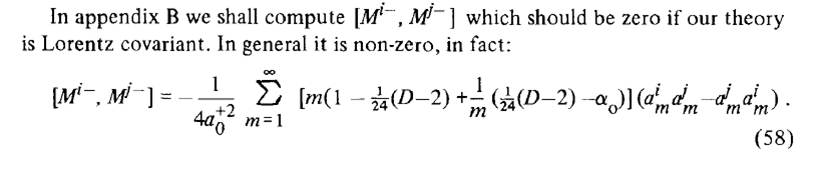



44 Comments
Très intéressant. Dommage qu’on ne puisse pas tweeter tes billets !
Euh…bonne remarque ! Je ne suis pas familier avec tweeter en fait. J’imagine qu’il faut que je rajoute un bouton quelque part sur le site ? Est-ce que ce cher WordPress.com fait ça ?
Bon on dirait que j’ai réussi, merci pour l’idée !
Ben voilà, c’est tweeté ! 😀
Pas nécessairement.
Partir du principe que notre perception explique le physique (ou la physique) est comme essayer d’expliquer à un être en 2D que la D3 existe.
Il aura probablement le même raisonnement.
Voire il pourra douter de l’existence d’êtres 3D.
Nos moyens de perceptions sont essentiellement limités à la détection d’une partie de plus en plus importante du rayonnement EM.
Est-ce suffisant pour affirmer que seul ce qu’on perçoit existe?
L’hypothèse de la matière et énergie sombre semblent dire que non.
Pourquoi on ne les verraient pas parce qu’elles sont d’une (ou plusieurs) autre(s) dimension(s)? Et, de la même manière que les 3D sont liées pour former un « espace » et « interagissent » entre elles, les autres dimensions pourraient « interagir » avec ce que nous nommons la 3D ou espace. Matière et énergies « invisibles » parce qu’elles ne sont pas dans notre construction mentale de l’espace.
Pas nécessairement pour ce qu’on nous enseigne sur la base de nos observations (puis établissements d’hypothèses pour en tirer des théories valides dans un certain contexte).
Évidemment, ce n’est que mon point de vue et je me garderais bien de l’affirmer de manière aussi « sonnante » que ce papier.
Super de faire le point sur ce que signifient ces 10 ou 24 dimensions.
Je suis tout à fait d’accord sur le caractère abstrait de certaines théories, mais cela ne signifie pas nécessairement que ces grandeurs sont inaccessibles et que l’on ne peut pas les mesurer. En ce qui concerne la fonction d’ondes, il est tout à fait possible de la mesurer, on peut citer en premier lieu le microscope à effet tunnel, qui permet de mesurer la fonction d’onde électronique à la surface d’un matériau, et , plus récemment, les expériences de tomographie quantique. Il en est de même de la métrique, que l’on peut mesurer avec des horloges et en échangeant des ondes électromagnétiques.
Merci pour ces précisions ! J’ai dû creuser un peu pour me convaincre que la phase de la fonction d’onde était effectivement accessible
http://quantum.quniverse.sk/buzek/zaujimave/p343_s.pdf
Pour la métrique je suis un peu troublé car j’avais en tête qu’il existe une famille de transformations géométriques qui modifient la métrique sans modifier la physique sous-jacente. Mais je n’arrive plus à remettre la main dessus.
http://web.mit.edu/edbert/GR/gr4.pdf
Bon j’aurai dû prendre des exemples plus compliqués d’objets mathématiques non-mesurables ! C’est de toute manière un peu la philosophie des théories de jauge, où on introduit un objet intermédiaire que l’on peut reparamétriser par une opération de symétrie sans changer la physique observable.
D’un autre côté on sait qu’on peut avoir accès au potentiel vecteur de l’electromagnétisme par l’effet Ahranov-Bohm, je ne sais pas si celui-ci se généralise à tous les types de théorie de jauge…Je suis un peu sec là-dessus.
salut, personnellement je crois que les autres dimensions a part les 3 connues sont » la temperature , la pression , le temps … » je pense que c’est des parametres physiques qu’il faut jouer sur et rien d’autre …
….
….
Étant donné que les 6 autres dimensions sont considérées comme des objets mathématique non-directement mesurable je pense qu’il ne sert a rien d’essayer de déterminer quel sont elles car ce ne sont pas elles même qui permettent de déterminer si la théorie des cordes est valable ou pas. Il faut parvenir a déterminer combien sont elles et si elles ont une véritable une influence sur cette théorie qui d’ailleurs me parait assez bancale faute de preuve convainquant .
Vouloir réécrire toutes la définition de la physique sur le plan quantique est probablement une bonne chose mais les progrès de ce siècle sont telle que a peine une une théorie est approuvée et Paf une autre est remise en question c’est ça la science : remettre en question
Le temps est déjà une quatrième dimension prise en compte.
La pression n’est que le rapport d’une force sur une surface, la température est une notion thermodynamique un peu plus difficile à définir en peu de mots, disons qu’elle est fonction de l’état microscopique du système.
Dans tout les cas, la pression et la température se ramènent par leur définition à des variables des dimensions spatiales et temporelles. Pour reprendre l’exemple de la pression, c’est l’équivalent d’une force sur une surface, la force étant elle-même la modification d’un vecteur vitesse (c’est à dire d’un rapport d’une distance sur un temps).
Pingback: Le boson de Higgs expliqué à ma fille « Science étonnante
Pingback: Le LHC peut-il fabriquer un trou noir au CERN ? « Science étonnante
Bonjour, ce sujet m’interpelle mais je suis nulle en physique. Il y aurait-il une bonne âme pour m’expliquer la théorie des cordes de manière simple et succincte?
Un peu en retard, car j’attendais de comprendre un peu mieux cette théorie pour pouvoir lire le billet. ^^
Voilà une vidéo de vulgarisation de cette théorie :
http://www.dailymotion.com/video/xi111_ce-qu-einstein-ne-savait-pas-encore_news
J’espère qu’elle t’aidera à mieux cerner le concept.
Bon voilà, j’ai enfn lu cet article ! 🙂 Personnellement, je trouve que la théorie des cordes est « bancale », qu’elle a trop de difficultés, si on peut dire ça. (Au fait, je pensais que c’était 11 dimensions, et pas 10 …) Je fait un copier/coller d’un message que j’avais posté sur un forum, où j’explique ce que j’en pense :
« J’ai regardé la vidéo de vulgarisation que […] a donné. Je suis la seule à trouver que cette théorie est … bancale (pas d’autre mot) ? Bon, c’est de la vulgarisation, j’en suis conciente, mais même, j’ai l’impression que c’est trop compliqué. Vous allez me dire que la physique c’est compliqué de toute façon, mais ce que je veux dire c’est que ça l’est trop. J’ai du mal à expliquer mes pensées la plupart du temps, alors je crois que je vais donner un exemple. (Déjà, connaissez-vous le rasoir d’Ockham ? Parce que, ce que je vais dire se base en quelque sorte dessus.)
Vous avez déjà entendu les théories sur le fait que la Terre est au centre du système solaire ? Cest théories qui explique pourquoi Mars « bouge » d’une manière bizarre ? Je dois dire que les théories sont quand même bonnes, même si on sait à présent que c’est la Terre qui tourne autour du Soleil. Elles pouvaient expliquer ce qu’on observait depuis la Terre. Ces théories là ont été changé et modifieé à plusieurs reprise pour « correspondre » à ce qu’on voyait. On rajoutait des « sphères » invisibles, etc… J’ai l’impression que c’est ce que fait la théorie des cordes. On rajoute des cordes et des dimensions pour expliquer les observations qu’on fait. Bien entendu (comme le fait que les sphères soit invisibles pour la théorie géocentrisme) les « cordes » sont invisibles car trop petites pour être observables.
Pour la théorie géocentrisme, le fait de mettre des sphères invisibles « compliquait » cette même théorie, alors que dire que la Terre tourne autour du Soleil, est plus simple.
Je crois que c’est la même choses pour cette théorie, où « rajouter » des cordes et des dimensions « complique » la théorie, et qu’en fait quelque chose de plus simple qui peut nous sembler inconcevable maintenant, qui c’est ? expliquerait de façon plus simple ce qu’on observe. Après, je n’ai pas de théorie qui puisse expliquer ça.
Après, je ne dis pas que j’ai raison, je suis bien conciente que je peux lourdement me tromper (surtout que je me base sur une vulgarisation) ; mais voilà mon avis. Vous en pensez quoi ?
Si ce n’est pas très clair, demandez des précisions, j’essairai de mieux expliquer ce que j’en pense. »
(Oui, j’ai eu la grande flemme de tout reécrire …)
C’est un peu (beaucoup) long, mais je ne crois pas que j’arriverai à faire plus court … Bon, voilà. ^^’
Je te réponds aussi en profane Daniella 😉
Quand bien même l’ajout de dimensions dans les modèles de théorie des cordes serait analogue à l’ajout d’épicycles dans l’astronomie pré-galiléenne, tu oublies un point important que voulez souligner l’article que nous commentons : ce sont des [i]modèles[/i] mathématiques.
Ils sont métaphysiquement neutres, ils ne prétendent pas dire ce qu’est l’essence du monde. Il se trouve que dans différentes formulations de théories des cordes pour que « cela marche » il faut introduire un espace à n dimensions avec n>4 (26, 11 10 dimensions selon les théories).
Peut-être que c’est bien le cas, l’univers a 10 dimensions, peut-être pas. L’objet de la physique n’est pas vraiment là, le but de ces théories est principalement d’unifier les deux grandes théories de la physique fondamentale contemporaine mécanique quantique et relativité générale et qu’importe je crois pour la plupart des physiciens le nombre de dimensions qu’il faille postuler pour cela.
D’une certaine façon, l’astronomie médiévale était dans la même situation. Le but principal était que les calculs astronomiques permettent de prédire avec le plus de précision possible les phénomènes célestes. Et quand Copernic a proposé l’hypothèse héliocentrique ce n’était que comme une commodité de calcul. Peu importe pour la plupart des savants de l’époque de savoir à quoi correspondent « réellement » les épicycles ou qui gravite « vraiment » autour de qui. (Par ailleurs, il y avait de solides raisons de refuser une interprétation réaliste de l’hypothèse héliocentrique, par exemple si toutes les planètes tournent autour du Soleil comment expliquer que la Lune gravite autour de la Terre plutôt que de s’y écraser ou de s’en arracher pour aussi graviter autour du Soleil ?)
De façon générale, les physiciens ont toujours préféré la théorie avec le plus grand pouvoir prédictif qu’importe qu’elle soit contre-intuitive. L’exemple le plus célèbre, c’est le succès de la théorie de Newton qui incluait une action à distance (la force universelle de gravitation) – ce qui sous un certain aspect ressemblait furieusement à un retour aux explications « magiques » contre lesquelles avaient lutté la physique mécanistique (n’admettant que l’action par contact). Cette dernière proposait bien un modèle (les tourbillons d’éther de Descartes) beaucoup plus « compréhensible » mais bien moins prédictif. D’où sa défaite.
Petite précision tout de même :
« Ces théories là ont été changé et modifieé à plusieurs reprise pour “correspondre” à ce qu’on voyait. On rajoutait des “sphères” invisibles, etc… J’ai l’impression que c’est ce que fait la théorie des cordes. »
Ce n’est pas le cas. La théorie des cordes ne repose que peu et très indirectement sur des observations. L’article ci-dessus explique assez bien quelle contrainte mathématique (la symétrie) impose « l’apparition » de dimensions supplémentaires.
La théorie des cordes vise avant tout à unifier mécanique quantique et physique relativiste qui sont incompatibles (par exemple la mécanique quantique peut autoriser un transfert instantané d’information ce qui semble violer la vitesse-limite imposé en relativité générale). Il existe bien des objets pour lesquels une telle théorie unifiée est cruciale, parce que leur comportement relève des des deux théories, à savoir les trous noirs.
Mais au-delà de l’étude de ces phénomènes, ce sont des motivations conceptuelles/théoriques, la passion pour l’unification, qui motivent l’entreprise.
Merci pour toutes ces précisions ! ^^ Je comprends mieux certains points, à présent. Je suis encore jeune, ce qui fait qu’il y a pas mal de choses que je n’ai pas encore vu, donc mes « théories » (ou je ne sais pas comment appeler ça) sont quand même très limités. Je vais voir ce que c’est « les tourbillons d’éther de Descartes », je crois déjà avoir vu ça quelque part …
La gravité, si je ne me plante pas, on ne sait pas encore à quoi elle est dû, non ? J’ai toujours trouvé ça un peu bizarre/spécial que la Terre ne « s’écrase » pas dans le Soleil, et la Lune dans la Terre … Enfin, je suis du genre à remmettre en cause toute les théories que je vois, xD. C’est idiot, en plus, j’ai pas le niveau pour le faire, mais je le fais quand même …
M’enfin bon, merci beaucoup ! 🙂
Pour ce qui est de la gravité, dans la théorie d’Einstein on la considère comme une déformation de l’espace-temps.
Mais il y a ce problème de la gravité quantique. En gros, les deux théories (relativité générale et physique quantique) reposent sur des postulats incompatibles et chacune fait d’excellentes prédictions à une échelle spatiale différente (respectivement macroscopique et microscopique). A l’échelle macro, c’est la gravité qui l’emporte sur les autres interactions. D’où l’efficacité explicative de la relativité générale à cette échelle. A l’échelle micro, nous n’avons pas d’instrument pour faire des mesures de la gravité, donc on ne sait pas trop ce qui se passe. Mais la physique quantique permet d’expliquer les autres forces en jeu à cette échelle. On aimerait bien qu’elle puisse aussi expliquer la gravité.
Pingback: D’où vient le boson de Higgs ? | Strip Science
interessant de lire tout ca ! que signifie exactement une dimension? a part les 3 qu’on peut imaginer , est ce que les autres dimensions dont on parle ont le meme sens que ces trois !!!! ou juste ce sont des parametres mathematiques independants l’un de l’autre.
imagine un monde ou tout est en deux dimensions, pour te donner une image imagine que tu es mario sur ces jeux de game boy color et que tu peux juste aller tout droit, reculer et sauter, et cela toute ta vie.
A quel moment est-ce que tu pensera qu’il est peut-être possible d’aller à droite ou à gauche?
il te sera difficile de l’imaginer car ton cerveau sera juste capable d’identifier les deux dimensions sur lesquels tu as évolué.
C’est de même pour nous, nous « vivons » dans un espace à trois dimension, il nous est pas conséquent très difficile d’imaginer une quatrième dimension spatiale s’ajoutant aux 3 que nous connaissons.
Pour ma part j’aime imaginer que lorsque nous prenons une fusée supposer aller très très vite, nous faisons qu’évoluer sur une sphère qui est l’univers, tout comme nous évoluons « scotchés » sur notre planète terre, l’univers serais alors une sphère sur laquelle nous pouvons juste évoluer en deux dimension, nous pouvons donc juste parcourir cette sphère et il y as, bien entendu un moment ou l’on reviendrais à notre point de départ. Du point de vue de la terre, cette quatrième dimension serait l’univers.
Je ne sais pas si j’ai été bien clair et si cela répond en partie à ta question, n’hésite pas au cas ou.
Pingback: 1+2+3+4+5+6+7+… = -1/12 ! | Science étonnante
Pingback: Pourquoi je n’aime pas le boson de Higgs | Science étonnante
Pingback: Matrice - dimensions | Pearltrees
Pingback: Reel (reel) | Pearltrees
Aux quatre dimensions connues de la matière. j’ajouterais une cinquième, soit la vie. C’est-a-dire que la matière connaît une propriété complémentaire, soit celle de se complexifier, de se mouvoir et de se reproduire. Une autre dimension de la matière (une sixième) serait l’intelligence. La matière peut penser, inventer les mathématiques, développer des technologies, etc.
Pensez-y
Bonjour, une dimension se traduit par coordonné, sur les dimensions spatiales ça peut-être négative ou positive et pour le temps tu ne peux décider que sur un temps enregistré
Exemple: Une vidéo.
Pour ceux spatiales, ils ont des axes, la longueur, la largeur, et la hauteur, et ont peut se déplacer au sens propre dessus, ces axes sont concrets, alors que sur un dessin tu ne peux dessiner l’intelligence, tu ne peux ni dessiner la vie (tu peux néanmoins faire des allégories), la vie est un produit de la matière, les dimensions sont immatériels
La théorie des cordes est une théorie et rien d’autre. Je ne pense pas que quelqu’un ai déjà expliqué que la réalité physique était celle-là.
Cette théorie tente d’unifier mécanique quantique et relativité. Mais la question que l’on peut se poser, et que à priori personne ne se pose, c’est que peut être l’une ces théories (ou les deux) est fausse ou partielle. La théorie des cordes peut mener à revoir la mécanique quantique ou la relativité générale.
J’ai lu sur ce blog un article « Les extraterrestres sont parmi nous »; Pourquoi pas. Mais alors ils ont laissés tombé la relativité générale depuis longtemps…
Pingback: La théorie des cordes | Science étonnante
Pingback: Espace / Temps | Pearltrees
Je sais que notre Univers possède bel et bien 12 dimensions… que les lois physiques changent avec la taille de notre » objet » d’étude… et qu’il y a deux nouvelles lois physiques qui seront bientôt découvertes au centre de notre galaxie grâce à un nouveau modèle de télescope avec une lentille au plasma… à suivre 🙂
Lorsque je lis des choses sur la théorie des cordes et ses fameuses dimension supplémentaires, il me semble explicite que ces dimensions renvoient à quelque chose « d’objectif », de réel. Par exemple, sur la page wikipédia des « dimensions supplémentaires », dans le cadre notamment de la théorie de Kaluza-Klein, il est question de l’histoire de ces dimensions, quand sont-elles apparus dans l’ère de Plank etc. Je veux dire qu’il semble qu’il ne s’agit pas de propriétés mathématiques, mais que ça renvoie à quelque chose. Pareil, lorsque vous évoquez la fonction d’onde et des concepts de ce genre, vous voudrez que les physiciens qui veulent expliquer le fonctionnement du monde mettent en évidence l’existence de choses qui ne correspondent à rien et intègrent ces informations dans des théories descriptives de la réalité? Ça me paraît très étrange.. C’est comme dire que l’ADN ne renvoie à rien, c’est juste un objet théorique permettant d’expliquer la diversité humaine, ça n’a pas beaucoup de sens..
Lorsque les physiciens s’évertuent à trouver des explications sur pourquoi on ne ressent pas ces dimensions, c’est bien qu’il est question d’une réalité objective, non?
Des gens dans les commentaires prenaient l’exemple de Copernic qui place la terre au milieu de l’univers car c’est pratique pour les calculs ; oui, mais à l’arrivée, la terre est au milieu du système solaire. À partir du moment où (même si on considère cela comme une fiction) on organise le monde de tel manière que ça nous permet d’expliquer un phénomène, cela a des implications réels, et si cette organisation s’avèrent fausses, la théorie est fausse, non?
Pour continuer sur Copernic, l’hypothèse de la position de la terre renvoie à quelque chose d’objectif, vrai ou faux, qu’il l’ait fait uniquement car c’était pratique mathématiquement, ça ne change rien.
Bon, je suis pas experte. C’est dit. Je vais peut-être dire une ânerie. Mais, jusqu’à ce qu’on se dise : Tiens ? Mais c’est quoi ? L’espace-temps ? C’est quelque chose ? On ne comptait pas « en dimension ». Ça nous en fait 4 d’un coup avec les 3 d’espace et celle de temps.
Et je me dis, les autres dimensions, on en a pas forcément conscience parce qu’on ne s’est jamais dit : Tiens ? Mais c’est quoi ? Ca ? C’est quelque chose ?
Et je pense, en disant ça, à l’Entropie. Une, peut-être deux dimensions d’un coup : Le désordre/l’ordre de toute chose et le hasard qu’on retrouve jusqu’aux probabilités quantiques. Présente partout, comme une pellicule collée à tout ce qu’on perçoit, jusque dans les trous noirs.
Après avoir relativement pris connaissance des différents commentaires, j’en suis parvenue a émettre une contre hypothèse sur le fait que le temps est une dimensions. J’en revient au commentaire laissé par un autre, le but n’est pas de trouver quelles sont les différentes dimensions mais de les énumérées. Ce que je tenais a exprimer avec toute franchise c’est qu’apparemment le temps en lui même n’existe pas au niveau macroscopique…
http://www.elishean.fr/le-temps-nexiste-pas/ (au passage c’est un très bon article)
Alors ma question est : dimensions ou pas ?
Pingback: Six mondes, Lokas et dimensions. - Coaching Intégral NOW1
Bonjour.
Sait on expliquer pourquoi le monde que nous expérimentons tous les jours est fait de 3 dimensions spatiales ?.
Pourquoi 3 et pas 4 ou 5?
Salutations
il peut-être fait de 4 ou 5 dimensions si les dimensions supplémentaires sont « recroquevillées », c’est-à-dire non représentables en « géométrie euclidienne » (avec un 4ème axe perpendiculaire aux précédents)
Bonjour à tous
Est-il possible que, si l’univers possédait 10 dimensions, les 6 manquantes soient les 5 sens ou ce qui les produits et la pensée ?
Bonsoir , Et si il y en avait beaucoup plus ? je pense personnellement que nôtre approche de la question n’est pas adapté a la tache escompter. il y a plusieurs facteurs a prendre en compte, tout d’abord est ce que le temps résulte même de l’expension de l’univers ?
L’univers pourrait etre ordonné d’une tel manière d’une géométrie tellement complexe tellement parfaite que personne ne pourrait en percé réellement le mystère , d’une multitude de dimensions se chevauchant les unes aux autres .
Chacune d’elle possédant sont propre temps, il y a certainement des fissures spatio-temporel dailleurs les trous noir en sont la preuve parfaite, qu’il y a t’il après l’horizon des évènements et encore après ?..
Pas facile de l’imaginer car il faut déjà se mettre en tête que l’univers est un amas de dimensions et a la fois chaotique en plusieurs endroit dont la cause principale serait les étoiles, MAIS les etoiles donne vie également alors je dirait plutôt que c’est un cycle sans fin éternel ou création et destruction se produisent a tout instant . une conception de temps différente n’est pas que chiffre au contraire, essayez plutôt de visualiser une couleur qui n’existe pas..
Impossible n’est ce pas? tout est question de point de vue , de perception , dans des dimensions bien supérieur a 10 qui est tout de même assez minime pour l’univers le temps n’existe pas, du moins de nôtre point de vue bien sur,
en réalité c’est comme si il y avait un mur infranchissable et que certains objets céleste pourrait percé la première couche de cet épais mur. On parle beaucoup de courbure moi ici je parle plutôt de perforation du temps et une nouvelle perception du temps , les génies de la science sont toujours sortie du lot avec des idées qui semblait impensable aux yeux des autres ( voici la perception ) et qui des année plus tard ce sont reconnu etre vrai.
bonjour
j’ai ce même point de vue. Les 3d de notre univers observables ne sont dues qu’aux interactions entre des particules ayant des dimensions propres, une particule embarque avec elles les dimensions des autres particules, définissables par des phases. Les 3d ne sont que le résultat de symétries et orthogonalités, dont les degrés de liberté n’expriment la présence des dimensions supplémentaires que sous la forme des paramètres dont on cherche l’origine (masse, charge…)
Par contre ce n’est pas l’expansion dont il faut parler, il faut considérer que l’horizon de notre univers observable grandit, qu’il intersecte toujours plus de matière avec l’univers infini inaccessible. Le temps consiste en un phénomène de propagation des propriétés de symétries et d’orthogonalité au travers des dimensions des particules sur l’horizon. Le nombre de particules étant important, il va falloir, à la physique, formaliser cette impression d’espace 3d continu
Mais non, ce n’est pas inaccessible, mais va falloir être assez fin sur les hypothèses parcequ’il faut mélanger des grand nombres et leurs inverses
Bonjour, j’aimerais bien que l’on m’explique la formulation en intégrale de chemin de la mécanique quantique bien la formulation de Palatini de la relativité générale de manière assez simple. Je suis en prépa et je suis très curieux de sciences donc ça m’intéresse vraiment !
Merci d’avance et bravo pour ce billet !