 Tous les liquides ne s’écoulent pas de la même manière. Si vous observez l’eau d’un fleuve, vous pouvez voir que son écoulement est en permanence le siège de multiples tourbillons. Au contraire, l’huile qui s’écoule hors d’une bouteille ne tourbillonne pas du tout.
Tous les liquides ne s’écoulent pas de la même manière. Si vous observez l’eau d’un fleuve, vous pouvez voir que son écoulement est en permanence le siège de multiples tourbillons. Au contraire, l’huile qui s’écoule hors d’une bouteille ne tourbillonne pas du tout.
Étonnamment, la frontière entre ces deux situations est assez mince, et on peut la percevoir au moyen d’une quantité appelée nombre de Reynolds. Comme nous allons le voir, la compréhension de la transition entre les deux comportements fait encore l’objet de recherches pointues [1].
La turbulence
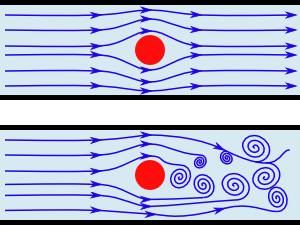 Quand l’écoulement d’un liquide est le siège de multiples tourbillons, on dit que cet écoulement est turbulent. Au contraire si l’écoulement semble se faire de manière bien parallèle, on parle d’écoulement laminaire.
Quand l’écoulement d’un liquide est le siège de multiples tourbillons, on dit que cet écoulement est turbulent. Au contraire si l’écoulement semble se faire de manière bien parallèle, on parle d’écoulement laminaire.
Les écoulements turbulents se repèrent particulièrement au voisinage d’obstacles, par exemple les piles d’un pont. La différence entre les deux situations est schématisée sur la figure ci-contre : en haut l’écoulement laminaire, en bas l’écoulement turbulent.
Ce qui fait la différence, c’est que dans un écoulement turbulent, les petites perturbations donnent naissance à des tourbillons. Au contraire dans un écoulement laminaire, les perturbations se résorbent rapidement et l’écoulement reprend son cours tranquille.
Comment savoir à l’avance si un écoulement va être le siège de turbulence ? Cela dépend principalement de la viscosité du liquide, car celle-ci agit comme un frottement qui va freiner les perturbations et empêcher les tourbillons d’apparaître. Mais à quel moment la viscosité est-elle suffisante pour freiner l’apparition des tourbillons turbulents ?
Une lutte entre viscosité et inertie
Pour savoir si la viscosité est assez forte pour freiner les tourbillons, il faut la comparer à l’inertie de l’écoulement. La viscosité tend à faire disparaître les tourbillons, alors que l’inertie les propage. Pour comprendre cet affrontement entre viscosité et inertie, prenons l’analogie avec un skieur (au lycée, en méca, il y a tout le temps des skieurs).
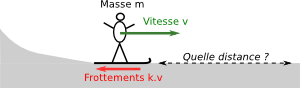 Vous êtes un skieur et vous arrivez en bas d’une pente, à un endroit où la piste devient plate. Quelle distance allez-vous parcourir sur le plat grâce à votre élan ? Évidemment, ça dépend : d’une part de la vitesse que vous avez acquise, et d’autre part de l’intensité des frottements qui vont vous freiner. Il s’agit d’une lutte entre votre inertie accumulée et les frottements de la neige.
Vous êtes un skieur et vous arrivez en bas d’une pente, à un endroit où la piste devient plate. Quelle distance allez-vous parcourir sur le plat grâce à votre élan ? Évidemment, ça dépend : d’une part de la vitesse que vous avez acquise, et d’autre part de l’intensité des frottements qui vont vous freiner. Il s’agit d’une lutte entre votre inertie accumulée et les frottements de la neige.
Pour quantifier votre inertie, on peut regarder votre énergie cinétique, qui vaut comme vous le savez \((1/2) m v^2\). Pour les frottements, on peut les exprimer sous la forme d’une force proportionnelle à votre vitesse, par exemple \(k.v\) où \(k\) est un coefficient de frottement.
Si vous faite le rapport des deux, vous obtenez \(mv/k\), qui est une quantité qui vous donne en gros la distance que vous allez parcourir grâce à votre élan. Si vous êtes lourd, rapide et que la neige glisse bien, vous irez plus loin que si vous êtes léger, lent et que la neige est de la soupe.
Le nombre de Reynolds
Retournons à notre liquide, et appliquons lui un raisonnement analogue au skieur. Imaginons que le liquide s’écoule à une vitesse moyenne v, dans un tube de diamètre D. Si \(\rho\) est la masse volumique du fluide, l’énergie cinétique du fluide est en gros proportionnelle à \(\rho v^2\).
Pour la viscosité, elle fonctionne presque comme les frottements du skieur. Pour faire simple, on peut dire que la viscosité est ce qui fait que le liquide a tendance à coller à la paroi du tube. Les forces de viscosité sont d’autant plus importantes que la viscosité \(\mu\) du liquide est élevée, que sa vitesse v est importante, et que le diamètre \(D\) du tube est petit. Au final, l’énergie dissipée par les forces de viscosité est proportionnelle à la quantité \(\mu v /D\)
Pour calculer le ratio inertie/frottement dans le liquide, on fait le rapport des deux formules que je viens de détailler, et on obtient cette quantité appelée le nombre de Reynolds de l’écoulement
\(Re = \frac{\rho v D}{\mu}\)
Ce nombre va nous permettre de détecter l’apparition de la turbulence : plus il est élevé, plus l’inertie est importante et la viscosité faible, et plus les tourbillons pourront se développer.
Quelques valeurs du nombre de Reynolds
Il faut faire deux observations importantes sur le nombre de Reynolds. La première est qu’il n’a pas d’unité. C’est en effet le rapport de deux quantités qui sont des énergies volumiques, et le résultat est donc un nombre sans dimension.
 La deuxième observation est qu’il ne dépend pas uniquement du liquide que l’on considère : il n’y a pas de sens à parler du nombre de Reynolds « de l’eau », puisque cela dépend des caractéristiques de l’écoulement (vitesse et diamètre du tube).
La deuxième observation est qu’il ne dépend pas uniquement du liquide que l’on considère : il n’y a pas de sens à parler du nombre de Reynolds « de l’eau », puisque cela dépend des caractéristiques de l’écoulement (vitesse et diamètre du tube).
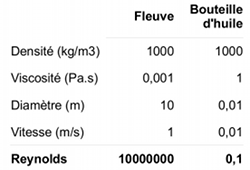
Reprenons les deux situations dont je parlais au départ : l’écoulement d’un fleuve et de l’huile d’une bouteille. Il ne s’agit pas vraiment d’écoulements dans un tube, mais on va faire comme si.
Le tableau ci-contre montre le calcul du nombre de Reynolds dans les deux situations. Vous pouvez constater qu’il est 100 millions de fois plus élevé dans le fleuve que dans la bouteille d’huile !
Pas étonnant que les tourbillons aient bien plus de chance de se développer dans le fleuve que dans la bouteille d’huile !
Une transition brutale
Bien que le nombre de Reynolds puisse varier de manière énorme d’un écoulement à l’autre, la frontière est entre l’écoulement laminaire et l’écoulement turbulent est en fait assez mince. On estime qu’un écoulement devient turbulent pour un nombre de Reynolds supérieur à 2000.
Ce nombre de Reynolds critique correspond en gros au moment où les forces visqueuses ne sont plus suffisamment fortes pour résorber les tourbillons. Comme vous pouvez vous en douter, la compréhension de cette limite entre turbulent et laminaire est d’une grande importance pour beaucoup d’applications technologiques, comme en ingénierie des procédés ou en aéronautique.
Une détermination précise du nombre de Reynolds critique
La valeur que j’ai donnée pour le nombre de Reynolds critique est en fait une approximation obtenue expérimentalement. Mais il est assez difficile de réaliser des écoulements dont la vitesse et la viscosité soient si bien contrôlés qu’on puisse observer avec précision la transition entre l’écoulement laminaire et l’écoulement turbulent.
Dans un article récent paru dans Science [1], des chercheurs ont réalisé une expérience très délicate pour déterminer avec précision ce moment critique où les perturbations deviennent des tourbillons qui subsistent au lieu de se résorber.
Pour cela ils ont créé un écoulement d’eau dans un tube de 4mm de diamètre et 15 mètres de long, à des vitesses autour de 0.5 m/s. Comme vous pouvez le vérifier, cela correspond justement à un nombre de Reynolds autour de 2000. Ils ont ensuite fait varier très légèrement la vitesse, et ont créé artificiellement des petites perturbations.
En observant l’amplification et la décroissance des perturbations, ils ont pu proposer une valeur précise pour le nombre de Reynolds critique, séparant le cas laminaire du cas turbulent : 2040. Ils sont même allés plus loin en étudiant précisément la manière dont les perturbations se développent, se propagent, voire se scindent. Les curieux peuvent aller voir l’article !
[1] A. Kavila et al., The Onset of Turbulence in Pipe Flow, Science 333, n°6039, p.192 (2011)
Billets reliés :
L’étrange viscosité des fluides non-newtoniens
Ce qu’il se passe pour les tous petits nageurs, qui ont un nombre de Reynolds très bas, traduit chez Dr. Goulu.


17 Comments
Pour ceux qui voudrait en savoir plus, le magazine Tangente dans son numéro 139, parlait du nombre de Reynolds dans deux articles :
– « la nage des micro-sous-marins » : c’était un article sur les travaux sur la natation optimale à faible nombre de Reynolds
– « un effet foot » : le célèbre effet Magnus qui dévie les tir brossé !
Mais votre article est très intéressent et à l’avantage d’avoir épuré les formules mathématiques : la formule dans l’article était la suivante : Re=(ρU²/R)/(μU/R²)=ρUR/μ pour une sphère de rayon R à la vitesse U dans un liquide de densité ρ et de viscosité μ, ce qui se rapproche beaucoup de votre formule !
Bonjour,
un bel effort de vulgarisation d’une notion pas si simple.
A quand la même chose pour le nombre de Mach (pour qualifier les différents régimes dans les écoulement d’air) et le nombre de Knudsen (idem pour les échanges thermiques? 🙂
Le nombre de Knudsen (http://fr.wikipedia.org/wiki/Nombre_de_Knudsen) sert à vérifier si un gaz est à une pression (ou densité) suffisante pour que l’on puisse le considérer comme un milieu continu. S’il est suffisamment faible (Kn < 0,01), on peut supposer que le gaz en question est bien un fluide au sens classique du terme, et le décrire de manière pertinente avec les équations "usuelles" (Navier-Stokes,…).
Il me semble que le nombre auquel vous faites référence est le nombre de Nusselt (http://fr.wikipedia.org/wiki/Nombre_de_Nusselt) qui sert à caractériser un échange de chaleur convectif, c'est-à-dire entre un fluide et un solide. En gros, le nombre de Nusselt est le rapport de la quantité de chaleur apportée par le fluide par convection, c'est-à-dire grâce à son mouvement, à celle qui transiterait au travers de ce même fluide par conduction thermique, c'est-à-dire en considérant que celui-ci est au repos.
La thermique et la mécanique des fluides regorgent de ce type de nombre sans dimension (nombre de Fourier, de Biot, d'Eckert, de Prandtl, etc.) qui sont souvent d'une très grande utilité lors de calculs pratiques se rapportant à des situations réelles.
C’est juste, mais le nombre de Knüdsen est effectivement aussi utile pour les échanges thermiques, car dans un matériau poreux, quand le libre parcours moyen des molécules d’un gaz devient de l’ordre de grandeur de la taille de porosité, la conductivité thermique chute.
C’est le principe à la base de la très basse conductivité des aérogels (qui sont microporeux) ou des panneaux isolants sous vide (la baisse de pression engendre une augmentation du libre parcours moyen).
Pingback: Voyage au centre de la Terre | Science étonnante
Question d’un pur béotien en la matière :
puisqu’en reprenant l’exemple d’une rivière, on pourra avoir un écoulement laminaire, ou turbulent.
Je suppose aussi que la vitesse d’écoulement de l’eau (soit la force du courant) et la largeur de cette rivière vont influer sur l’apparition ou non de turbulences.
Mais je pense également qu’avec des rivières où ces caractéristiques sont proches (vitesse d’écoulement et largeur) on pourra avoir dans un cas des turbulences, et dans l’autre « aucune ».
Il y a enfin la viscosité… mais de l’eau, c’est de l’eau! La viscosité est la même… qu’est-ce qui va provoquer ce changement de comportement?
En fait pour les rivières, il me semble qu’on sera toujours en régime à grand nombre de Reynolds, et donc turbulent. Pour autant on ne va pas forcément noter visuellement de grands tourbillons, mais l’eau ne s’écoulera pas de manière laminaire.
Pingback: La mystérieuse équation de Navier-Stokes | Science étonnante
Pingback: Comment les insectes font-ils pour voler ? | Science étonnante
Merci beaucoup !! j’ai interro demain et je pense avoir beaucoup appris 🙂
est ce que le nombre de Reynolds est directement proportionnel a la viscosité du liquide
oui il est proportionnel à la viscosité du liquide
Bonjour,
Merci pour votre article fort bien rédigé.
Je me permet de vous citer dans un site qui traite de la réalisation d’une pico turbine hydroélectrique et plus particulièrement dans la section dédiée aux pertes de charge : https://hydroturbine.info/formules-et-calculs/pertes-de-charge/pertes-de-charge-lineaires/
Cordialement,
Laurent
Bonjour
Nous sommes en prépa scientifique MPSI au lycée Pierre Corneille à Rouen, et dans le cadre de notre TIPE (Travaux d’initiative personnelle) sur le thème « L’océan », nous étudions la stabilité de structures en mer, et sommes à la recherche de bibliographie et éventuellement de conseils ou de contacts.
Nous souhaitons réaliser un modèle réduit d’une structure étudiée dans un bassin de 1m50 de long et d’une cinquantaine de centimètres de profondeur pour tester l’influence des vagues (amplitudes et fréquences) sur la stabilité de notre structure.
Nous souhaitions initialement travailler sur le Polar Pod (structure verticale destinée à réaliser des mesures en mer), dont l’objectif est de minimiser les oscillations verticales et latérales, mais en l’absence de bibliographie nous songeons à changer de structure étudiée.
Nous sommes donc à la recherche de renseignements sur la réalisation de modèles réduits en mer (le coefficient de Reynolds doit il intervenir dans l’établissement de notre structure ?) ainsi que de conseils quant à la structure à étudier.
Nous sommes bien conscients du peu de temps que vous êtes susceptible de nous accorder, et vous remercions vivement pour tout conseil ou contact que vous auriez.
Bien sincèrement
Léa, Louis, Camille
Comment se développe l’écriture [ ( v . grad ) v ] qui correspond à l’inertie newtonienne du fluide ?
Faut-il faire d’abord le produit vectoriel de la vitesse par le Nabla et appliquer le système d’écriture de coordonnées ainsi obtenu à la fonction V ? En quoi est-il du second ordre alors ?
Ou faut-il faire un autre développement ?
Oui on commence par faire le produit scalaire et ensuite on applique l’opérateur ainsi obtenu.
Les démonstrations de ce cours sont vraiment claires et accessibles ! Superbe! J aimerais avoir les mêmes démonstrations avec les démonstrations d un véhicule et d un avion aux différentes voire grandes vitesses dans l air ! Pénetrations dans du laminaires au turbulences voire tourbillonnaires et forces de trainées! Il y a bien sûr des démos interressantes sur des sites mais ici elles sont vraiment … limpides!! Merci Thank you merci a vous et à Tous!