 On fête cette année les 100 ans de la découverte de la supraconductivité. Cet anniversaire est l’occasion de voir un peu partout cette merveilleuse expérience où un aimant lévite au dessus d’un supraconducteur.
On fête cette année les 100 ans de la découverte de la supraconductivité. Cet anniversaire est l’occasion de voir un peu partout cette merveilleuse expérience où un aimant lévite au dessus d’un supraconducteur.
Je me suis souvent demandé en quoi le fait de conduire le courant sans résistance était responsable de ce phénomène de lévitation. Je ne l’ai appris que bien plus tard, et la réponse est : en rien !
Dans ce billet, je vais tenter de faire un peu la lumière sur ces phénomènes, et montrer en quoi une résistance électrique nulle n’est ni nécessaire ni suffisante pour léviter dans un champ magnétique.
Qu’est-ce qu’un conducteur électrique parfait ?
Commençons par les classiques : on sait que dans un conducteur électrique, l’intensité et la tension sont reliées par la loi d’Ohm I = U/R. L’intensité I représente en gros la vitesse des électrons qui forment le courant, et la tension U est la force qu’on leur applique pour les faire bouger. Plus cette force est élevée, plus leur vitesse est importante. Quant à la résistance R, elle représente les frottements que subissent les électrons, à cause de collisions dans le matériau.
Un conducteur parfait, c’est un matériau dont la résistance électrique est nulle. Mais que devient la loi d’Ohm quand R=0 ? Pour le comprendre, il est utile de se mettre à la place d’un électron, et de prendre une analogie mécanique : la chute libre.
La chute libre
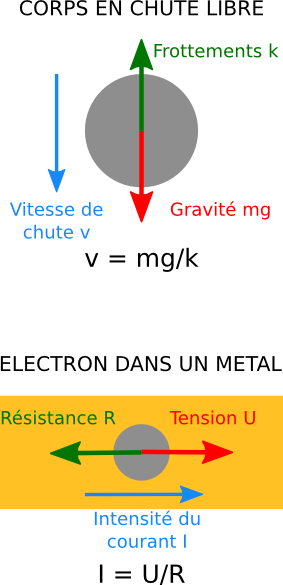 Si vous vous jetez d’un avion à altitude suffisamment élevée, vous allez tomber vers le sol pendant un moment. Vous subissez deux forces : la gravité qui vous fait tomber, et les frottements de l’air qui vous freinent. On considère en général que la force de frottement est proportionnelle à la vitesse avec un coefficient de frottement k.
Si vous vous jetez d’un avion à altitude suffisamment élevée, vous allez tomber vers le sol pendant un moment. Vous subissez deux forces : la gravité qui vous fait tomber, et les frottements de l’air qui vous freinent. On considère en général que la force de frottement est proportionnelle à la vitesse avec un coefficient de frottement k.
Si on écrit la loi du mouvement (« masse x accélération = somme des forces »), on obtient
\(m\frac{dv}{dt} = mg – kv\)
Si vous résolvez cette équation (ou simplement si vous la regardez bien), vous verrez qu’elle vous dit que dans votre chute, vous allez atteindre une vitesse limite \(v = {mg}/{k}\). Cette équation présente de grandes similitudes avec la loi d’Ohm ! Elle relie votre vitesse à la force qui vous met en mouvement (la gravité) et aux frottements que vous subissez.
Maintenant, pour comprendre ce que vit un électron dans un conducteur parfait, reprenons le raisonnement de la chute libre en prenant un coefficient de frottement nul k=0. L’équation du mouvement est alors simplement dv/dt = g. Ça n’est plus la vitesse qui est proportionnelle à la force de gravité, mais l’accélération. Donc dans une chute libre sans frottements, la vitesse n’est plus limitée et peut devenir aussi élevée que l’on veut.
Pour un électron dans un conducteur de résistance nulle, ce sera pareil ! Sa vitesse n’est plus limitée par les frottements, et elle peut devenir aussi élevée que l’on veut, même pour une tension fixée. La loi d’Ohm n’est plus valide (et pour les curieux, on a en fait une loi du genre dI/dt = U).
La découverte de la supraconductivité
 Nous savons que dans un conducteur normal, la résistance représente les frottements subis par les électrons, principalement à cause de leurs collisions avec le réseau cristallin dans lequel ils se déplacent. Il est légitime de penser que ces collisions doivent diminuer quand la température baisse, car le réseau est alors moins agité. On peut donc imaginer que la résistance d’un matériau va tendre vers zéro quand la température est abaissée vers le zéro absolu. C’est cette hypothèse qu’a voulu tester le néerlandais Kamerlingh Onnes en 1911.
Nous savons que dans un conducteur normal, la résistance représente les frottements subis par les électrons, principalement à cause de leurs collisions avec le réseau cristallin dans lequel ils se déplacent. Il est légitime de penser que ces collisions doivent diminuer quand la température baisse, car le réseau est alors moins agité. On peut donc imaginer que la résistance d’un matériau va tendre vers zéro quand la température est abaissée vers le zéro absolu. C’est cette hypothèse qu’a voulu tester le néerlandais Kamerlingh Onnes en 1911.
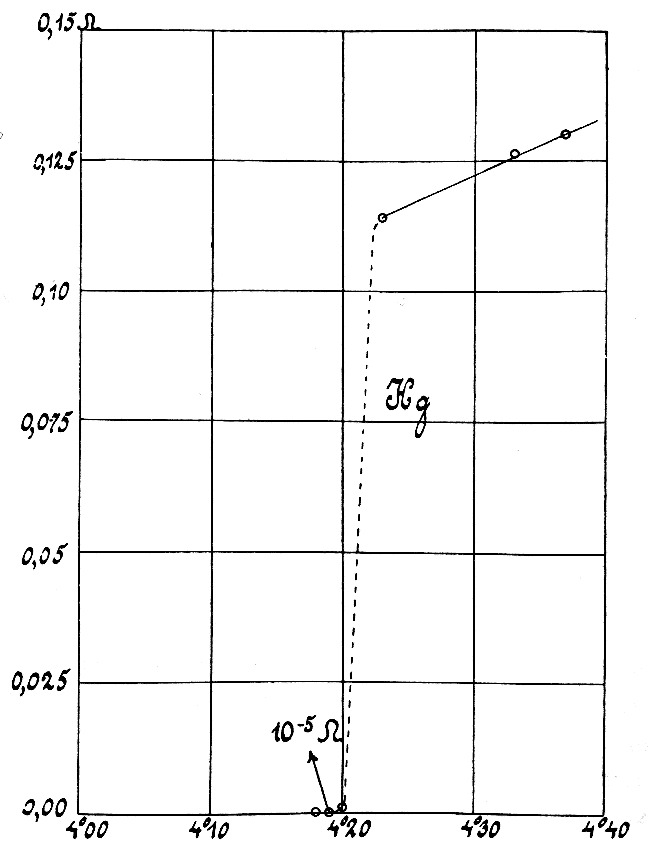
Pour étudier cette dépendance de la résistance en fonction de la température, Onnes s’est servi de mercure refroidit à l’hélium liquide. La courbe qu’il a obtenu est reproduite ci-contre : la résistivité en fonction de la température. Contrairement à ce qu’on aurait pu attendre, la résistivité du mercure ne diminue pas progressivement, mais devient brutalement nulle lorsque l’on passe en dessous d’une température, dite « critique », de 4.2 K. Le mercure devient supraconducteur.
Ce phénomène montre qu’il est bien possible de supprimer complètement les frottements qui créent la résistance électrique, mais d’une manière brutale, et donc différente de ce qui était attendu à l’époque.
L’effet Meissner
En 1933, Meissner découvre un autre phénomène : il montre qu’un supraconducteur peut léviter au dessus d’un aimant (ou l’inverse) ! Précisons-le clairement : il s’agissait à l’époque d’un effet inattendu. A priori, rien ne permettait de prédire qu’un supraconducteur allait léviter dans un champ magnétique. Donc si vous ne voyez pas le rapport entre les deux, c’est normal !
L’expérience de Meissner est très importante, car elle montre qu’un supraconducteur, ça n’est pas juste un conducteur parfait de résistance nulle. C’est quelque chose en plus. On peut dire que c’est aussi un matériau qui lévite dans un champ magnétique. Pour comprendre l’origine de la lévitation, nous allons nous intéresser au fonctionnement des aimants, et au comportement magnétique des matériaux en général. Et vous aller voir que la lévitation n’a absolument rien de spécifique aux supraconducteurs !
La lévitation magnétique
 Pour commencer, la lévitation magnétique n’est ni magique, ni exotique : il est parfaitement possible de faire léviter un aimant sur un autre. Il suffit de mettre leurs pôles en opposition. Évidemment ce dispositif n’est pas stable, car les aimants ont tendance à essayer de se retourner pour se coller. Mais si vous les contraignez, par exemple en les enfilant sur une tige, la lévitation se fait sans problème. Comme dans le petit jouet représenté ci-contre.
Pour commencer, la lévitation magnétique n’est ni magique, ni exotique : il est parfaitement possible de faire léviter un aimant sur un autre. Il suffit de mettre leurs pôles en opposition. Évidemment ce dispositif n’est pas stable, car les aimants ont tendance à essayer de se retourner pour se coller. Mais si vous les contraignez, par exemple en les enfilant sur une tige, la lévitation se fait sans problème. Comme dans le petit jouet représenté ci-contre.
Comment cela fonctionne-t-il ? Prenons le cas de seulement deux aimants. Si l’aimant du dessus lévite, c’est parce que la gravité qui le fait tomber est compensée par une force magnétique qui le repousse. Pour faire simple, cette force magnétique est proportionnelle à l’intensité des champs magnétiques créés par chacun des deux aimants. De plus, si les deux champs sont dans le même sens, c’est une force attractive, s’ils sont opposés, c’est une force répulsive.
Maintenant, voyons le cas d’un aimant avec un objet normal, qui n’est pas aimanté. Le point clé est le suivant : quand un matériau subit un champ magnétique extérieur, il va répondre en créant à son tour autre un champ magnétique, dit champ induit. Cela signifie qu’un matériau normal devient un aimant s’il est en présence d’un autre aimant. On dit que les matériaux sont magnétiquement « susceptibles ».
Quand nous avons deux aimants, nous avons donc deux champs magnétiques. Et si nous avons un aimant et un matériau normal, nous avons aussi deux champs magnétiques : celui de l’aimant et celui qui se forme dans l’autre matériau du fait de sa susceptibilité. Pour savoir si cela peut créer de la lévitation, il faut regarder un peu mieux cette histoire de susceptibilité.
Les différents types de susceptibilité magnétique
Si on applique un champ extérieur (noté H) à un matériau, celui-ci va donc réagir de manière susceptible en créant son propre champ magnétique, noté M. L’important est que cette réaction est proportionnelle au champ extérieur appliqué , de sorte que M = XH: le coefficient de proportionnalité X est appelée la susceptibilité magnétique du matériau.
On distingue alors 3 cas :
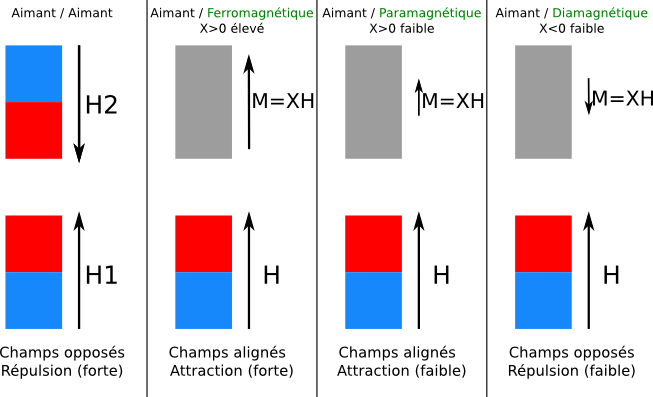
- X est positif, et élevé : dans ce cas le matériau est dit ferromagnétique. Il répond au champ magnétique en créant un second champ magnétique dans le même sens. C’est le cas du fer, et c’est pour cela qu’il est attiré par l’aimant. Rappelez-vous : quand les deux champs sont dans le même sens, la force magnétique est attractive !
- X est positif et faible : on parle de matériau paramagnétique. En principe ces matériaux sont aussi attirés par l’aimant, mais en pratique le champ induit est tellement faible que ça ne se voit pas.
- X est négatif et faible : le matériau est dit diamagnétique. Le champ induit est opposé au champ extérieur, et donc la force magnétique est répulsive. La plupart des matériaux sont en fait diamagnétiques, et donc repoussés par les aimants. Mais en pratique, là aussi l’effet est tellement faible que la répulsion ne se voit pas.
Le schéma ci-dessous résume les 4 cas que nous venons de voir :
 La lévitation des diamagnétiques
La lévitation des diamagnétiques
Vous voyez que l’idée de diamagnétisme contient la clé pour léviter : un matériau diamagnétique répond à un champ magnétique avec une force répulsive. Mais je vous l’ai dit, l’effet est en général tellement faible qu’il est impossible de compenser la gravité et donc de véritablement léviter. Impossible ? Sauf si l’objet est léger et que le champ magnétique extérieur que l’on applique est très très élevé.
Et figurez vous que l’eau est justement un matériau diamagnétique. Donc en principe, dans un champ très fort, elle peut léviter ! C’est ainsi que des chercheurs facétieux ont pu faire léviter une grenouille dans un champ magnétique énorme : 16 teslas. La vidéo ci-dessous le montre.
[youtube=http://www.youtube.com/watch?v=A1vyB-O5i6E]
Si vous cherchez, vous pouvez aussi trouver des vidéos de la lévitation d’une souris, ou simplement d’une goutte d’eau.
Le supraconducteur : un super-diamagnétique
Nous sommes presque à la fin de notre épopée. J’ai listé ci-dessus 3 cas : ferromagnétique, paramagnétique, diamagnétique, suivant que la susceptibilité est forte ou faible, et positive ou négative. Si vous êtes observateur, vous voyez qu’il manque un cas : celui où la susceptibilité est négative et élevée ! On appelle cela le superdiamagnétisme. Sauf qu’on ne connait aucun matériau de ce genre…à part justement les supraconducteurs !
Les supraconducteurs sont des superdiamagnétiques ! Ils répondent de manière forte et opposée à un champ magnétique extérieur. Et c’est pour cela qu’ils peuvent léviter au dessus d’un aimant, sans qu’il y ait besoin d’un champ énorme comme pour la grenouille.
En fait, leur susceptibilité est même exactement égale à -1. Ce qui veut dire que leur champ induit M est exactement égal à –H, l’opposé du champ qu’on leur applique. Donc le champ total dans un supraconducteur (qui est la somme du champ extérieur H et du champ induit M) est nul ! C’est pour cela que l’on entend parfois que les supraconducteurs « expulsent le champ magnétique ». Mais cette affirmation m’a toujours paru plutôt énigmatique, et c’est pour cela que j’ai souhaité écrire ce billet. J’espère que cela vous aura éclairé aussi.
En conclusion, retenez donc ce qu’est un supraconducteur. C’est la réunion de deux propriétés : conduction électrique parfaite ET superdiamagnétisme.
Pour aller plus loin
Pour une description phénoménologique simple d’un supraconducteur sans avoir à se taper la théorie BCS, je conseille aux plus motivés d’aller jeter un oeil aux équations de London. Il y en a deux : la première équation de London est l’exact équivalent de la chute libre sans frottements. Elle décrit le conducteur parfait. La seconde équation implique la propriété de superdiamagnétisme, puisqu’elle a pour conséquence que le champ magnétique total est nul (sauf en surface du matériau). Le point important est que ces deux équations sont bien indépendantes : un conducteur parfait n’est pas nécessairement superdiamagnétique.
Toutefois, j’exagère un peu en soulignant que les deux propriétés sont totalement indépendantes. Il faut dire que pour être superdiamagnétique, ça aide d’être un conducteur parfait. On peut le comprendre d’une façon simple. Dans un matériau « normal », un champ magnétique extérieur provoque un déplacement des électrons d’une manière qui crée un champ magnétique induit qui s’oppose au champ magnétique initial. C’est un phénomène du type loi de Lenz. Donc être diamagnétique, c’est le comportement normal d’un matériau. Pour être superdiamagnétique, il faut que les courants induits puissent circuler le plus librement possible, pour que le champ induit soit suffisamment important. On considère d’ailleurs que si un supraconducteur arrive à expulser le champ extérieur, c’est parce que des petites boucles de courant se forment à sa surface et induisent un champ opposé que le compense.


36 Comments
Et on ne connait pas de conducteur parfait qui ne soit pas superdiamagnétique ?
la susceptibilité du meilleur matériau diamagnétique connu, le carbone pyrolytique est -0.0004, contre -1 pour un supraconducteur.
Soit un facteur 2500 ! Mais du coup s’il est léger, on peut quand même le faire léviter au dessus d’un bon aimant : voir ici http://en.wikipedia.org/wiki/File:Diamagnetic_graphite_levitation.jpg
La première image me semble être un morceau de supraconducteur (probablement YBa2Cu3O7) lévitant au dessus d’un aimant et non l’inverse.
J’avoue que je me suis demandé. Comme ça avait l’air de fumer en dessous, j’en ai conclu que le supra était en dessous. Mais je peux me tromper !
le supra est en bas. il est refroidi dans de l’azote liquide. il n’y aurait pas d’intérêt à refroidir l’aimant permanent. l’aimant permanent est comme encollé. c’est sûrement pour éviter qu’il casse s’il tombe. les aimants néodyme sont puissance mais très fragiles…
Je rebondis sur la fin du paragraphe « la chute libre ».
La vitesse des électrons dans le matériau supraconducteur n’est-elle pas bornée par celle de la lumière ?
Ah ben j’ai lu, et je suis tout confus, maintenant !
Déjà naïvement je me disais : c’est normal, magnétisme → boucles de courant induit dans le supraconducteur → magnétisme, ça doit se calculer ; tu commences par annoncer que non non, on peut pas montrer que supraconducteur implique super-diamagnétique, et à la fin tu sembles dire que pour finir mon idée naïve pourrait être la bonne… je suis perdu !
Et puis tu dis que les deux choses sont indépendantes, mais en te lisant on a le sentiment que tous les supraconducteurs sont super-diamagnétiques, et inversement ! Ça s’appelle « équivalent », chez moi !
Et alors, dI/dt = U dans un supraconducteur… euh… alors I = Ut ?! Mais qu’est-ce qui empêche que ça parte à l’infini ?! Je suppose que cette loi n’est pas valide indéfiniment ?!
Bon je vais essayer de clarifier alors ! Attention à bien comprendre ce que j’appelle un « conducteur parfait » (un matériau de résistivité nulle), et la différence avec un « supraconducteur » (le truc obtenu en dessous la température critique).
Je dis que « léviter » et « être un conducteur parfait » sont deux choses indépendantes. On peut léviter sans être un conducteur parfait (la grenouille), et, en principe, on peut être un conducteur parfait sans léviter (je n’ai pas d’exemple matériel mais les lois de la physique semblent le permettre).
En outre « conducteur parfait » n’implique pas « super-diamagnétisme » (susceptibilité -1). Par contre ce que j’explique à la fin, c’est que conducteur parfait, ça ne peut que aider pour avoir une susceptibilité très négative. Mais ça n’explique en rien le fait que ce soit -1, et que donc le machin « expulse » le champ.
La question ouverte pour moi, c’est est-ce que « superdiamagnétique » implique « conducteur parfait ». J’ai envie de dire que non. Techniquement, on peut vérifier la deuxième équation de London sans satisfaire la première. Mais là non plus, pas d’exemple matériel sous la main.
Je vais être un peu formel sinon on va jamais se comprendre. Je note m un machin quelconque, R(m) sa résistance et X(m) sa susceptibilité.
Tu affirmes qu’on n’a pas R(m) = 0 ⇔ X(m) = -1, et même qu’on n’a ni R(m) = 0 ⇒ X(m) = -1, ni X(m) = -1 ⇒ R(m) = 0.
Je dis que pour nier chacune des implications, il faut exhiber un m1 avec R(m1) = 0 et X(m) > -1, et un m2 avec X(m2) = -1 et R(m2) > 0 — oui oui, j’ai été constructiviste… si on n’a pas de tels exemples, si on ne sait pas en construire, on en est réduits à un aveu d’ignorance, non ?
Oui, tu as raison de formaliser. C’est exactement ce que je veux dire.
Il me semble que l’on a effectivement pas de contre-exemple. Même si pour autant que je le comprenne, ces contre-exemples sont permis dans l’état actuel de notre compréhension des lois physiques.
« The possibility of the existence of superdiamagnetism in non-superconducting substances is discussed. »
On the problem of superdiamagnetism
« A perfect conductor without the special quantum properties of real superconductors is known as a classical superconductor. No such materials are known to exist, though the concept is a useful idealization of the low-resistivity case in many systems »
Perfect conductors
Je ne sais pas ce qu’il faut en conclure du coup !
J’avais loupé cette réponse, merci !!
Bonjour.
Je ne comprends pas trop pouvais vous m’aider à y voir plus claire svp ?
Un matériel supraconducteur laissera les électrons se déplacer comme bon leur semble sans frottement donc très peu de chaleur OK.
Qui dit supraconductivité dit résistance inférieur à 0.
Mais logiquement plus la résistance est nul plus le matériel pourra induire du courant et donc une force électromagnétique non ? Car celle ci est proportionnel au courant induit dans le matériel. Lorsque un courant traverse un fil de cuivre par exemple celui ci créer automatiquement un champs magnétique
Merci d’avance
Sur wikipédia, dans l’article http://fr.wikipedia.org/wiki/Supraconductivit%C3%A9, à la fin de la section « Effet Meisner », il y a une note que je reproduis ici :
certains supraconducteurs, dits de type II, ne présentent l’effet Meissner que pour de faibles valeurs du champ magnétique, tout en restant supraconducteurs à des valeurs plus élevées (cf. infra).
Est-ce que ça ne veut pas dire que dans certaines conditions on a la résistance nulle sans le superdiamagnétisme ?
Oui c’est vrai : lorsque le supraconducteur est en présence d’un champ magnétique trop « intense », il n’arrive plus à créer un champ magnétique assez intense pour s’y opposer, donc il ne lévite plus (mais sa résistance intérieure reste nulle)
Pour mieux comprendre, je vous conseille d’aller lire ceci : http://www.supraconductivite.fr/fr/index.php?p=supra-levitation-meissner
Moi aussi je suis comme chouettesavantes: totalement embrouillé! Déjà, je croyais que seuls les supraconducteurs étaient des conducteurs parfaits (première erreur) et ensuite, que l’effet Meissner (un champ magnétique toujours nul au sein d’un supraconducteur) était une simple conséquence de la conductivité parfaite: deuxième erreur. Au moins ce soudain brouillard a le mérite de démasquer les fausses évidences, c’est déjà pas mal!
Pour te désembrouiller, je te conseille vraiment d’aller lire les équations de London, qui décrivent phénoménologiquement les supraconducteurs, et se dérivent de la théorie BCS.
http://en.wikipedia.org/wiki/London_equations#Original_arguments
La première équation traduit la conduction parfaite. Elle dit en gros que la dérivée temporelle du courant est proportionnelle au champ électrique (mon dI/dt = U)…
Si on prend le rotationel de la première équation, on obtient une équation sur le champ B, dont la solution montre que le champ B est constant dans le matériau (sauf dans une fine couche en surface).
Si on impose comme condition supplémentaire que le champ B est constant ET nul, on obtient la seconde équation de London, qui décrit donc l’effet Meissner.
Donc :
* un conducteur parfait vérifie la première équation
* un matériau superdiamagnétique vérifie la seconde.
Les deux équations sont indépendantes pour autant que je le comprenne, donc on peut imaginer que l’on puisse être conducteur parfait sans être superdiamagnétique, et réciproquement. Maintenant effectivement, ça ne prouve pas que de tels matériaux existent vraiment.
Bon en fait ça veut peut-être dire aussi que le travail n’est pas fini : nous avons un fait empirique (pas de matériaux qui sont superdiamagnétiques sans être supraconducteur, et vice-versa) qu’on ne sait pas prédire ni expliquer avec la théorie ; soit on bosse pour améliorer nos prédictions et nos explications (et peut-être la théorie), soit on bosse (en utilisant la théorie) pour produire les fameux matériaux manquants….
Et tu n’as pas répondu sur I = Ut, c’est vraiment comme ça ?! En fait en pratique on est limité par le générateur (qui n’est pas supra conducteur, et a donc une résistance), je suppose ?
Est-ce qu’on peut faire une dynamo avec des matériaux supraconducteurs ? Je le suppose, on fait des électro aimants supraconducteurs… et si j’ai bien compris on arrive à fermer le circuit sans générateur, le courant continue à « tourner » à l’infini ?
Ah oui pour I = U.t…
Eh bien ce que dit exactement la première équation de London, c’est en gros que la dérivée temporelle du flux J est proportionnelle au champ électrique E.
J’ai l’impression que dans un supraconducteur (qui satisfait les 2 équations de London), on doit pouvoir montrer que (de même que pour le champ B), le champ E doit être nul sauf dans une fine couche en surface. En bidouillant London et Maxwell, ça doit se faire…mais là je n’ai pas le courage d’essayer !
En complément, jolie vidéo (merci Mathieu !) démontrant le caractère paramagnétique de l’oxygène liquide : http://www.youtube.com/watch?v=jiXQKAwoRLY
je suis tombé sur cette science fascinante en …cherchant …tout simplement… je ne connai rien à la science mais je me demandai comment les O.V.N.I pouvaient ce déplacer dans les ciel, et, si il se pourrait qu’il y est un lien avec ce genre d’études que j’admire énormément!!
Bonjour,
Pour I=U.t, c’est facile : U=0, et t=infini, donc I peut prendre la valeur que l’on veut…
Plus serieusement, effectivement, quand on joue avec les équations de Maxwell et l’équation de London, on trouve que le champ E doit être nul, sauf dans une couche fine en surface, comme B, ou comme j d’ailleurs.
Je trouve que vous donnez un peu trop de signification différente aux deux équations de London, j’ai tendence à les mettre dans le même panier, et moyennant quelques hypothèses on peut passer de l’une à l’autre (ce que fait l’article de wikipedia d’ailleurs). Je reformulerais le probleme ainsi : Quand vous avez un conducteur parfait (R=0), vous ne pouvez plus utiliser la loi d’Ohm pour decrire le comportement des électrons libres dans ce métal, il vous manque une équation. Si vous ajoutez l’équation de London, alors vous trouvez un système (Maxwell+London) qui décrit bien le comportement des supraconducteurs, et notemment l’effet Meissner. A priori, rien n’interdit l’existence d’autres systemes où la loi d’Ohm est remplacée par une autre relation, à condition que le tout soit cohérant bien entendu. On aurait alors la description d’un système conducteur parfait, sans l’effet Meissner (et donc, qui ne décrirait pas l’état supraconducteur). Bon, je chipotte, excusez moi…
La supra, c’est quand meme vachement compliqué, mais c’est vraiment un beau sujet de mécanique quantique, et des expériences vraiment impressionnantes, surtout quand on a la chance de pouvoir les voir en vrai. Heureusement que les fetes de la sciences permettent souvent de les découvrir !
Pour compléter les informations de l’article, les supraconducteurs de types II ne sont plus des diamagnetiques parfaits, effectivement, mais présentent bien une resistance électrique nulle. Leur physique est passionnante (un nouveau billet ?), mais que je trouve assez difficile à expliquer clairement. En gros, pour certains supras, le systeme « gagne » de l’énergie en cessant d’être supraconducteur le long de « tunnels » qui traversent le matériau, tunnels qui sont traversés par un quantum de flux magnétique. De cette façon, le matériau peut rester supraconducteur presque partout (sauf dans ces régions, les « vortex ») jusqu’à des champs magnétiques plus élevés, puisque n’étant plus un diamagnétique parfait il a moins de champs magnétique à expulser. En gros. Le département de physique d’Oslo propose de nombreuses images des ces vortex, une très jolie galerie à découvrir ici : http://www.mn.uio.no/fysikk/english/research/groups/amks/superconductivity/
Merci pour toutes ces précisions. Effectivement je n’ai pas parlé des « types II », mais les images de l’équipe d’Oslo sont en effet très chouettes !
Pour le caractère inter-dépendant des équations de London, je ne suis pas sûr d’être d’accord, ce qui évidemment m’embête un peu vu que tu as l’air de travailler dans le domaine 🙂
Pour moi la première équation
http://upload.wikimedia.org/wikipedia/en/math/4/5/8/458aee59631d58f0031204ef6297778f.png
décrit un conducteur parfait, mais à elle seule n’explique pas l’effet Meissner.
Je ne vois pas comment on peut déduire la seconde équation de London à partir de la première. En revanche à partir de la première et de Maxwell, je vois bien comment obtenir
http://upload.wikimedia.org/wikipedia/en/math/b/5/1/b51527caa72137a949864dfca55b55b6.png
qui n’est pas la seconde équation de London mais sa dérivée par rapport au temps. Appelons la 1,5ème équation de London.
Donc pour autant que je le comprenne, si on se limite à la 1ère équation de London, on peut déduire la 1.5ème, mais pas la 2nde 🙂 Pour avoir la seconde, il faut un ingrédient supplémentaire (qui me semble indépendant de tout le reste), c’est de dire que dans la 1.5ème équation, ça n’est pas simplement la dérivée par rapport au temps qui est nulle, mais bien tout le terme entre parenthèses.
J’ai l’impression que si on se limite à la 1ère (et que donc on a la 1.5ème), on a le résultat que dans un conducteur parfait le champ B ne peut pas varier. Donc si il est nul quand on passe dans l’état supraconducteur, alors il doit le rester et dans ce cas on peut avoir de la lévitation. En revanche dans ce cas si le champ B est non-nul au moment où on passe dans l’état supra, alors il reste non-nul et le supra n’est pas capable d’expulser le champ. Pour avoir l’expulsion d’un champ créé avant le passage dans l’état supra, il faut la 2nde équation de London.
Il me semble donc que la manip discriminante serait de poser un aimant sur une céramique supraconductrice au dessus de sa Tc, puis de la refroidir. Si la céramique expulse l’aimant quand elle devient assez froide, c’est qu’il faut bien la seconde équation et pas uniquement la première.
Est-ce que je me trompe quelque part ? 🙂
Bonjour,
J’ai en effet pas mal réfléchi à la supra, mais ça ne m’empêche pas de dire des bêtises à l’occasion…
En fait, je suis d’accord et pas d’accord avec vous. Voilà qui va faire avancer le schimblick.
En prenant vos notations, oui, la première équation de London traduit une résistance nulle, et oui la seconde est nécessaire pour trouver l’effet Meissner. Vous avez tout à fait raison. D’accord également pour votre interprétation de la 1.5ème équation. Actuellement, il me semble que la tendance dans les livres est de parler d’une seule équation de London, et d’utiliser celle qui donne j en fonction de A.
Là où je ne vous suit pas est que vous donnez l’impression que tout matériau présentant une résistance nulle suivra forcément ce que vous appelez la première loi de London (et que je n’appelle pas !). Je suis d’accord pour dire que cette équation traduit une résistance électrique nulle, mais dans un modèle bien précis (Drude). Je prends un contre exemple, mais attention, je ne suis pas un spécialiste : l’effet Hall quantique. Dans ce régime (2D, semicon, basse température, haut champ magnétique, bref, un truc courant), on retrouve une situation où la résistance électrique tombe à zéro, mais pour des raisons fondamentalement différentes d’un supraconducteur. Je ne vois aucune raison pour que « la première équation de London », pour reprendre la terminologie wikipedia, soit vérifiée.
Excusez-moi si je vous donne l’impression de couper les cheveux en quatre. Je vais reformuler ma remarque : « Vous vous interrogez sur l’existence d’autres systèmes que les supraconducteurs présentant une résistance électrique nulle. En voici un, l’effet Hall quantique, qui, me semble-t-il, ne vérifie pas la première équation de London, car ce système est très loin du domaine d’application du modèle de Drude dont découle plus ou moins cette équation ».
(pause)
Je me permets également de rebondir sur l’expérience que vous présentez en fin de post (un aimant sur un supra, on refroidit le tout). Cette expérience en gros permet de faire la différence entre un supraconducteur (expulsion du champ magnétique) et un conducteur parfait (loi de Lenz : aucune variation du flux magnétique). En principe, je suis d’accord, et cette expérience a été réalisée la première fois en 1947 je crois :http://www.nature.com/physics/looking-back/arkadiev/index.html
En pratique, il faut faire cette expérience avec un supra de type I. Avec un supra de type II, l’expulsion du flux n’est plus totale, car il y a des vortex (qui portent un flux magnétique) traversant l’échantillon. Pour compliquer le tout, ces vortex vont avoir un comportement de physique hors-équilibre, avec des configurations métastables, et une hystérésis magnétique plus ou moins marquée. Selon l’amplitude de cette hystérésis, si vous faites l’expérience que vous proposez, tous les résultats sont possibles : soit l’aimant lévite (hystérésis magnétique faible, le diamagnétisme -non total- soulève l’aimant), soit l’amant ne bouge pas du tout (hystérésis forte, le flux magnétique de l’aimant est piégé dans le supraconducteur). La conclusion un peu contradictoire est que bien qu’on présente souvent les supraconducteurs comme étant fondamentalement différents d’un conducteur parfait (ce qui est vrai), souvent des effets métastables les font se comporter comme des conducteurs parfaits !
Un dessin vaut mieux qu’un long discours :
type II, faible hystérésis magnétique :
http://www.supraconductivite.fr/fr/index.php#supra-levitation-meissner
type II, forte hystérésis magnétique :
http://www.supraconductivite.fr/fr/index.php#supra-levitation-piegage
Où comment en apprendre plus sur les supras que ce qu’on aurait souhaité… Désolé pour la logorrhée!
Merci pour cette réponse détaillée !
Alors effectivement, il semble que l’effet Hall quantique soit effectivement le contre exemple qu’on cherchait. Je suis d’accord que ma vision de la première équation de London soit effectivement très imbibée de modèle à la Drude.
Et encore bravo pour le site sur la supraconductivité, et de manière générale tout ce qui a été fait pour l’année de la supra. La dernière conférence que j’ai vu sur le sujet par un de vos collègues m’a totalement bluffé !
je ne suis pas physicien et je ne comprend pas pourquoi l’élément qui lévite ne tombe pas sur les bords du supraconducteur ?
Ben c’est normal, c’est loin d’être une question facile… En fait, ça dépend du type de supraconducteur (I ou II, sans vortex ou avec).
Si vous utilisez un supraconducteur de type I, il n’y a pas de vortex, et vous êtes dans l’état Meissner pur. La seule force entre votre aimant et le supraconducteur est une force de répulsion. Les expériences qui utilisent ce genre de supra :
a) se font à des températures proches du zéro absolu, car les supra de type I connus ont des températures d’apparition de la supraconductivité en dessous de 10 kelvins. Il faut donc manipuler de l’hélium liquide, se qui se fait rarement en public (compliqué).
b) utilisent des supraconducteurs ayant la forme d’un bol, de façon a stabiliser la lévitation de l’aimant, et éviter qu’il tombe sur les bords du supraconducteur, comme vous le faites remarquer.
exemple : la lévitation d’un aimant au-dessus d’un bol en plomb, refroidi à 4.2 K.
http://fr.wikipedia.org/wiki/Fichier:Floating_Magnet..jpg
Si vous utilisez un supraconducteur de type II, il y a des vortex, et la force entre l’aimant et le supraconducteur peut être répulsive ou attractive, car une force supplémentaire intervient, la force de piégeage (des vortex). Cette force de piégeage peut stabiliser la lévitation d’un aimant au-dessus d’un supraconducteur plat. Quand cette force est élevée, il est même possible de faire léviter un aimant *en dessous* d’un supraconducteur. Toutes les expériences réalisées avec de l’azote liquide utilisent des supraconducteurs qui sont de type II.
exemple :
http://www.youtube.com/watch?v=nWP941PeexQ&list=UUrz6yN1bOc14v6WgXOV4LEQ&index=35&feature=plcp
Pingback: La localisation d’Anderson « Science étonnante
Bonjour,
Savez-vous si des étudiants ou chercheurs réalisent des expreriences ouvertes aux étudiants de classes préparatoires (sur paris) ? Ceci m’interesserait grandement, notamment dans le cadre de mon épreuve de TIPE!
Merci!
Bien cordialement.
Oui il faut regarder le travail de Julien Bobroff à Paris Sud
http://hebergement.u-psud.fr/supraconductivite/
Il a fait une conférence sur le sujet qu’il a fait tourné dans de nombreux lycées. Je l’ai vu une fois, c’est littéralement renversant ! A voir absolument !!
Pingback: Quantum | Pearltrees
Attention, Science Étonnante,
tu écris ici que l’intensité du courant électrique représente en gros la vitesse des électrons, mais cela est fourvoyant, je trouve, car l’intensité indique la quantité d’électrons se déplaçant et non leur vitesse. Cette dernière est appelée (à mon avis de façon peu heureuse) « vitesse de dérive » de l’électron.
Je pense tu devrais corriger, car cela fausse un peu aussi ta comparaison avec la chute des corps : en effet un corps en chute libre dans le vide voit augmenter sa vitesse à fur et à mesure de la progression de la chute, tandis que l’intensité du courant électrique dans un conducteur à résistance nulle est immédiatement maximale du départ, juste limitée par la capacité électromotrice du générateur dans le temps (y compris par sa résistance interne qui normalement existe toujours, mais j’ignore qu’en serait-il d’un éventuel générateur construit avec des seuls supraconducteurs relié à un fil supraconducteur…) ou autrement limitée par la perte de supraconductivité du conducteur, j’imagine, pour des courants excessifs. Au revoir.
Marco
Salut David je suis étudiant électrotechnicien en deuxième année au G15, au Senegal.
je prépare mon mémoire d’ étude sur la supraconductivité et je veux réaliser la lévitation magnétique au jj. j’ai déjà de l’azote liquide et il me reste seulement la pastille céramique.
je suis pas dans les meilleurs conditions nécessaires pour l’acheter directement en ligne.
J’attends de vous a ce que vous m’aidez pour que je puisse l’avoir plus facilement.
A part ca je tiens a vous remercier infiniment de tous ces sacrifices que vous endurez jours et nuits pour la promotion de la science et plus précisément la physique quantique domaine qui me plais beaucoup… au travers votre chaine youtube / votre site web / et votre page facebook.
Merciiii
Bonjour,
Je suis étudiant en CPGE PSI. et j’ai décider de faire un TIPE sur les supras qui sont complexe mais passionnant. la résistivité nul entraine le conducteur parfait (moi dans mon bouquin sur le modèle de drude donc j’ai un métal parfait c’est gamma qui tend vers l’infini donc l’épaisseur de peau tend vers 0 ce qui a pour effet de expulsé tout les champs en surface. mais le fait d’expulsé tout les champs en surface ne crée donc pas le diamagnétisme parfait et donc la lévitation ? De ce que j’ai lu plus haut vous essayer de dissocier ou d’associer les deux… ?
qu’est ce qui crée un diamagnétisme parfait ou en quoi on défini un diamagnétisme parfait ? parce que on dit un supraconducteur est un diamagnétisme parfait mais j’arrive pas a caractériser ce que c’est. alors que un metal parfait c’est clair, on a R=0 ou gamma=+oo.
Merci d’avance pour vos réponses
Aubin
Pingback: Son fonctionnement | Supraconductivité 1re S TPE
Pingback: La lévitation des supraconducteurs | 13 ...
Pingback: Avatar: Can a world like Pandora exist? - SHKMGMCNUH