 Dans ce billet nous allons voir en quoi l’existence de la musique occidentale repose sur le fait que 3 puissance 12 est (presque) égal à 2 puissance 19 ! Et pour cela, construisons un piano !
Dans ce billet nous allons voir en quoi l’existence de la musique occidentale repose sur le fait que 3 puissance 12 est (presque) égal à 2 puissance 19 ! Et pour cela, construisons un piano !
Le principe est simple : on va partir d’une première corde, dont la vibration produit une certaine note, et on va chercher successivement à construire les autres cordes du piano. Notre critère étant d’introduire de nouvelles cordes dont les sons « vont bien » avec ceux des cordes que l’on possède déjà.
Et voyons où cela nous mène !
Notre première série de notes
Imaginons que nous disposions pour commencer d’une corde tendue. Une corde qui vibre produit un son dont la fréquence dépend de sa longueur, de sa masse et de sa tension. Plus la corde est longue et massive, plus la vibration sera grave; plus la corde est tendue, plus le son sera aigu. Supposons que notre corde de départ vibre naturellement à une fréquence de 131 Hz. Cette vibration produit un son plutôt grave, appelons cette note « Do ».
Pour chercher des notes qui « vont bien » avec notre note de départ, on va se référer à la physique des vibrations. En effet on sait que si un objet vibre naturellement à une certaine fréquence F, il a tendance à également vibrer un peu à la fréquence double, 2F, c’est-à-dire dans dans notre cas 2 x 131 = 262Hz.
On comprend cela assez bien en observant une vraie corde et ses modes de vibration :
La conséquence de cela est d’une part que les sons produits à ces deux fréquences vont parfaitement aller ensemble, et d’autre part que notre oreille ressent ces deux sons de manière très analogue : on va d’ailleurs leur donner le même nom « Do ». On dit que le deuxième Do est « une octave plus haute » que le premier.
Nous avons une nouvelle note qui va bien avec notre note initiale : on décide donc d’ajouter une seconde corde (plus courte, plus tendue ou plus légère) qui vibrera à 262Hz.
Mais évidemment en répétant le raisonnement, une corde à 524 Hz ira parfaitement avec celle à 262 Hz, et une corde à 1048 Hz avec celle à 524 Hz, etc. Pour construire notre piano, on décide donc de fabriquer toute une série de cordes à ces fréquences :
131, 262, 524, 1048, 2096, 4192, etc.
Une deuxième série de notes
Nous avons vu que physiquement si une corde vibre à la fréquence F, elle vibrera aussi un peu à la fréquence 2F. Mais pour les mêmes raisons, elle vibrera aussi légèrement à la fréquence 3F. On peut donc regarder ce qu’on obtient comme note en fabriquant une nouvelle corde à la fréquence 3 x 131 = 393Hz.
A l’oreille, la note obtenue à cette fréquence produit une sensation clairement différente des précédentes, mais qui s’accorde très bien avec notre note initiale. On dit que cette nouvelle note (que l’on appellera Sol) est la quinte du Do.
Mais bien entendu avec cette nouvelle note, on peut aussi appliquer le premier principe et multiplier (ou diviser) la fréquence par 2 pour construire toute une nouvelle série de cordes, qui seront donc tous des « Sol ».
On décide ainsi d’ajouter à notre instrument une série de cordes aux fréquences suivantes :
197, 393, 786, 1572, 3144, 6288, etc.
A ce stade, on a retrouvé un certain nombre de notes du piano : tous les Do (en rouge) et tous les Sol (en vert). Le Sol ayant été construit pour « bien aller » avec le Do.
D’autres séries de cordes
Évidemment on peut maintenant itérer notre petit jeu, et construire une troisième série (qu’on appellera les Ré) correspondant à la quinte du Sol, puis une quatrième série, et ainsi de suite de proches en proches. Mais on s’arrête quand ?
Eh bien figurez vous qu’au bout d’un moment se produit un petit miracle : alors que vous venez de construire votre 12ème série de cordes (les Fa), dont les fréquences sont en gros : 177, 354, 692, 708, 1416, vous appliquez à nouveau la petite règle de la multiplication par 3, et là vous tombez sur les fréquences suivantes :
133, 265, 531, 1062, 2124, etc.
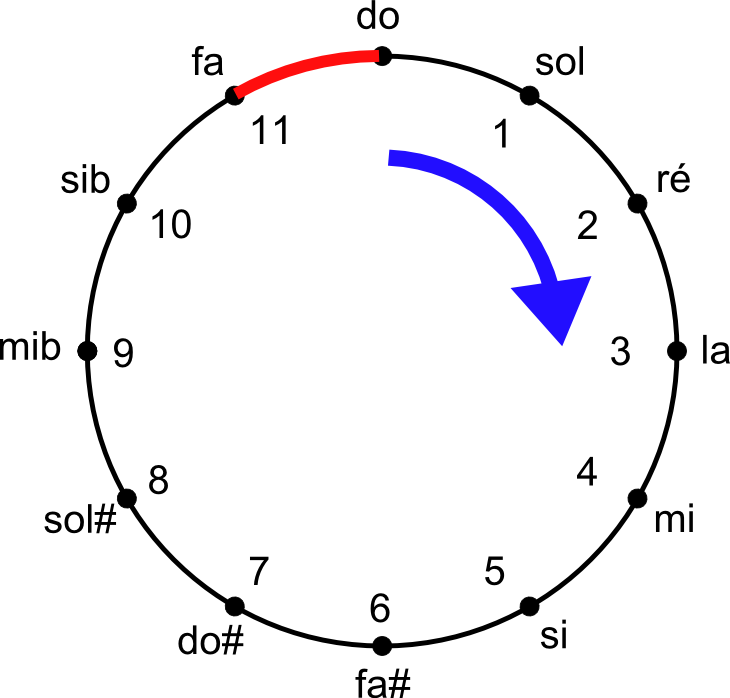 Et là, alors que vous vous apprêtiez à construire votre 13ème série de cordes, vous réalisez que les fréquences de cette 13ème série sont très très proches des fréquences de la première série !
Et là, alors que vous vous apprêtiez à construire votre 13ème série de cordes, vous réalisez que les fréquences de cette 13ème série sont très très proches des fréquences de la première série !
Musicalement, cela signifie que l’on cherche à construire la quinte du Fa, mais que cette dernière se trouve être quasiment le Do initial.
Et c’est là que la musique occidentale prend cette décision déterminante : considérer qu’effectivement le Do est quasi la quinte du Fa, qu’il n’y a pas besoin de rajouter une 13ème série de cordes, et que la boucle est bouclée ! C’est ce qui est symbolisé sur le diagramme ci-contre qui montre le cycle des quintes. Au bout de 12 applications de la règle des quintes, on retombe sur la note initiale.
Reprenons l’arithmétique
Si on reprend l’arithmétique de la construction précédente, on s’aperçoit que le petit miracle qui fait qu’on retombe sur ses pieds à la 12ème itération provient en fait de la (presque) égalité arithmétique 3 puissance 12 = 2 puissance 19. C’est grâce à cette relation qu’en suivant le cycle des quintes 12 fois on finit par retomber sur des notes que l’on a déjà construite, et qu’on peut donc arrêter d’ajouter des nouvelles notes.
En fait, en pratique, plutôt que de laisser à la douzième itération le soin de combler à elle seule le léger écart, on décide de le répartir sur l’ensemble de la gamme. Cela évite qu’il y ait certains intervalles de la gamme qui sonnent plus faux que les autres (ce qu’on appelait le « loup » sur les anciens instruments). C’est-à-dire que sur un instrument moderne, pour construire la quinte d’une note, on ne va pas multiplier sa fréquence par 3 mais plutôt par 2^(19/12). Et tout ça passe inaperçu à l’oreille, car
2^(19/12) = 2.9966
Il est formidable de voir que ce miracle se produit après 12 itérations, ce qui permet tout de même d’avoir un nombre de notes suffisant pour faire des jolies choses, sans pour autant être astronomique, pour garder des instruments raisonnables !
Peut-on construire des musiques alternatives ?
Si l’on est un puriste, on peut considérer qu’après la douzième itération la boucle n’est pas exactement bouclée, et que l’on veut continuer à ajouter des séries de cordes jusqu’à avoir une proximité encore plus grande.
Eh bien dans ce cas il faut attendre la 41ème ou la 53ème itération ! En effet on a
2^(65/41) = 3.0008
2^(84/53) = 2.99988
On pourrait donc s’imaginer construire des instruments (et donc une musique) basée sur 53 notes (au lieu de 12). Bon il faudrait des pianos à près de 380 touches !
Si vous êtes matheux et que voulez aller encore plus loin, vous pouvez bien sûr chercher d’autres approximations rationnelles de ln(3)/ln(2), car c’est bien de cela qu’il s’agit ! Pour les trouver, le mieux est de passer par un développement en fractions continues (485/306 marche bien aussi…) Pour ma part, je retourne écouter JJ Goldman…






27 Comments
Super bien expliqué, comme d’habitude…! Même quand on a déjà vu ça on te lit avec plaisir.
Super ! ça fait au moins une dizaine d’années que j’essayais (en vain !) de comprendre pourquoi il y avait 12 notes, pourquoi on devait se contenter d’arrondir légèrement certaines notes « pour que ça colle », etc !!!
et là, avec cet article lumineux, en 5 minutes, j’ai tout compris !
Merci ! merci ! merci !
Mais… la musique orientale, la musique indienne… comment fonctionnent-elle ?
Il semblerait que la majorité des musiques du monde soient plus ou moins sur le même système. D’après Wikipédia http://en.wikipedia.org/wiki/Musical_scale#Non-Western_scales voici quelques exceptions : la musique indonésienne, la musique arabe ‘maqamat’.
Apparemment en musique arabe, on utilise volontiers le quart de ton. Quant à la musique indonésienne jouée sur cet instrument appelé « gamelan », je cite
the tuning varies so widely from island to island, village to village, and even gamelan to gamelan
Tout un monde musical à découvrir…
Pas que dans la musique arabe : la musique turque utilise également le quart de ton (qui n’en est pas vraiment un du point de vue mathématique, sans compter qu’il a des valeurs différentes selon le contexte).
Dommage que vous ne soyez pas allé un poil plus loin pour nous parler des différents tempéraments anciens (pythagoricien, mésotonique, les multiples tempéraments inégaux de l’époque baroque, etc.) car c’est là que ça devient intéressant. Il aurait était intéressant également d’avoir une explication sur les commas. A ce propos d’ailleurs, il existe un article très intéressant : http://xavier.hubaut.info/coursmath/doc/thmus.htm
Pingback: Quand la musique est bonne, 3^12 = 2^19 | Ecoute et paysage sonore | Scoop.it
Salut D., je trouve ton article très clair, il m’aurait bien aidé à comprendre ces notions si je l’avais lu il y a quelques années.
Je me permets d’apporter un petit complément, sur les accords parfaits. Partant du do à 131 Hz, les harmoniques suivantes (aux arrondis près) sont à 262 Hz (do à l’octave supérieure), 392 Hz (sol), 523 Hz (do à l’octave encore au-dessus), 654 Hz (mi), 785 Hz (sol) ; d’où l’accord « parfait » do-mi-sol (qui n’a en fait rien d’arbitraire et qui est très physique).
Excellent article! et je souscris entièrement au commentaire de Don Quichotte.
Mais il y a un bémol 😉 Le 2 et le 3 on comprend d’où ils viennent et le 12 c’est la longueur du cycle des quintes mais le 19? J’avoue ne pas avoir compris.
Une manière de le dire autrement : tu pars d’une note de départ, et tu multiplie sa fréquence par 3 et au bout de 12 fois, tu tombes sur une note qui est presque pile 19 octaves au dessus de ta note de départ.
Souvent, on le trouve présenté d’une manière un peu différente : on passe à la quinte en multipliant par 3/2, et dans ce cas parcourir le cycle revient à monter de 7 octaves (3/2)^12 = 2^7.
Cet article super bien fait écho à un exercice que j’avais lu dans un bouquin de Physique de classe prépa, de M. Garing, qui essayait d’expliquer la physique des notes et la construction des gammes.
Joli billet. J’ai deux questions.
1) Je reprend une partie du billet : « La conséquence de cela est d’une part que les sons produits à ces deux fréquences vont parfaitement aller ensemble ». Pourquoi est-ce une conséquence ? Parce que ces associations de fréquences sont naturellement fréquent autour de nous et que sans cette conséquence notre environnement sonore nous paraîtrait toujours laid ?
2) On prendre des quintes successives, autrement dit on multiplie la fréquence initiale par des puissances de 3′. Mais ne serait-il pas naturel également de multiplier la fréquence par 5 ou 7 par exemple ? Mais peut-être ne récupère-t-on pas de nouvelles notes ainsi, il faudrait que je calcule…
Pour 1), j’avoue que je ne sais pas trop…pourquoi est-ce que deux sons à l’octave sonnent pareil, peut être parce que notre cerveau est habitué à « sentir » des rapports de fréquence ?
Pour 2), très bon point que je n’ai pas eu la place de développer 🙂 Effectivement si tu multiplies par 5, pour les mêmes raisons tu auras une note qui sonnera bien avec la fréquence de départ. On appelle cette note la « tierce ». Or il se trouve que la note obtenue ainsi n’est pas très loin de celle que tu obtiens en appliquant 4 fois le cycle des quintes.
« La quinte de la quinte de la quinte de la quinte » est quasiment la tierce.
Et derrière ça aussi il y a un petit miracle arithmétique, c’est que
3^4 = 5 * 2^3
(c’est à dire 81 presque égal à 80)
Pour 7 ça doit être pareil, mais je n’ai pas la note (une sixte ?) ni la valeur en tête…je vais chercher !
Un merci (tardif !) pour cette réponse.
Bonjour, et merci pour ce billet très clair sur le sujet.
Si je puis me permettre de répondre pour la 7e harmonique,
je dirais qu’elle correspond à l’intervalle de 7e de dominante, avec
3^10=7*2^13,
identité plus jolie si on l’écrit « à l’envers » en descendant le cycle de quinte :
7*3^2 = 2^6.
(c’est-à-dire 63 presque égal à 64 !)
Très joli, merci beaucoup !!
1) Je n’explique rien. Mais si ce n’étais pas le cas, il n’y aurait pas d’oreille absolue. Il faudrait regarder de ce coté je pense.
Merci pour ces explications. Je vais voir mon piano d’une autre façon désormais…
Pour tenter de répondre à ahaha, lorsqu’on joue au piano un do, on entend distinctement, contenu dans ce son, le do de l’octave supérieur, même si on ne joue pas ce dernier, car c’est sa première harmonique. On peut d’ailleurs faire l’expérience suivante: on frappe la touche du do tout en appuyant tout doucement sur la touche du do à l’octave, assez doucement pour ne faire que libérer la corde en décollant le marteau, celle ci se met à vibrer en résonance avec le do situé à l’octave inférieur. Donc, je pense que d’une part la sensation d’équivalence entre les octaves vient du fait que le do du bas contient dans son timbre de manière audible la note située à l’octave supérieure, comme si cette note à l’octave faisait partie de sa définition, de sa nature. D’autre part, comme on pourra m’opposer que, malgré tout, toutes les harmoniques de ces deux notes ne sont pas superposables, qu’il existe une « différence », je pense qu’il y a également une part éducative. Un musicien débutant ne reconnait pas forcément immédiatement et naturellement, sans un minimum d’apprentissage, l’intervalle correspondant à l’octave. L’équivalence de l’octave reste une convention qu’il faut s’approprier.
L’intervalle le plus consonant qui suit est la quinte, normal, c’est la deuxième harmonique qui est elle aussi contenue, et éventuellement audible (surtout quand on prend comme note fondamentale un son grave) dans ce son fondamental. Et ainsi de suite. Plus les harmoniques sont éloignées plus elles seront dissonantes en formant un intervalle.
D’ailleurs l’un de ces intervalles,très dissonant, le triton (do-fa# par exemple) pourtant si utilisé de nos jours dans la musique tonale était appelé diabolus et interdit formellement par l’église dans la musique du moyen age! 🙂
Quand on sait que l’harmonie d’un blues n’est assise que sur des intervalles de triton, il eut fallu aux chanteurs de l’époque baisser d’un ton pour exprimer leur désarroi !
Pingback: Blog Audio 2: Science Étonnante – Quand la musique est bonne, 3^12 = 2^19
Le rapport ln(3)/ln(2)
fait penser aux fractales et aux lois de puissance
http://www.sur-la-toile.com/discussion-227049-1-La-musique-classique-a-un-rythme-mathematique..html
http://classes.yale.edu/fractals/Panorama/Music/OneOverFMusic/OneOverFMusic.html
Alors, la musique serait-elle aussi conséquence d’un code source à trois faces, à l’instar du triangle de Sierpiński,
http://fr.wikipedia.org/wiki/Fractale
Ne retrouve-t-on pas ce triplet dans ces anneaux borroméens, » une » information livrée par un référent (le support de la note jouée), un signifiant (la note jouée), un signifié (la note que je ressens) ?
La mathématique, la vie, l’art, auraient-ils une architecture commune ?
Rectification
http://www.sur-la-toile.com/discussion-227049-1-La-musique-classique-a-un-rythme-mathematique.html
Rectfication :
La physique, la vie, l’art, auraient-ils une architecture commune ?
Pingback: Les 7 merveilles de la mécanique quantique | Science étonnante
Pingback: Le test de Turing-Parker : un ordinateur peut-il improviser comme Charlie Parker ? | Science étonnante
Pingback: Fiches thématiques | Pearltrees
Cette vibration que l,on retrouve dans certaine musique me collecte à mon moi supérieur et me fais composé ma poésie à leur écoute.Ça doit être pour ça que je suis né un 12
Pingback: Quand la musique est bonne, 3^12 = 2^19 | glana...
Pingback: Kosiwczw | Pearltrees