 Ces derniers temps, le nouvel accélérateur de particules du CERN a beaucoup fait parler de lui avec la chasse au boson de Higgs.
Ces derniers temps, le nouvel accélérateur de particules du CERN a beaucoup fait parler de lui avec la chasse au boson de Higgs.
Mais souvenez-vous qu’il y a quelques années, à l’époque de la construction du grand collisionneur LHC, une polémique existait sur les dangers d’un accélérateur de particules si puissant, et notamment sur le risque potentiel d’y créer des trous noirs.
Dans ce billet, je vous propose de voir en quoi certaines théories comportant des dimensions supplémentaires d’espace-temps conduisent à la prédiction que des trous noirs pourraient être créés au CERN.
Rassurez-vous, au menu d’aujourd’hui, il n’y aura ni théorie des cordes sauvage, ni formules mathématiques obscures, mais juste des estimations d’ordres de grandeur réalisées à l’aide de ce qui devrait être le couteau suisse de tout bon physicien : l’analyse dimensionnelle !
Quelle énergie faut-il pour créer un trou noir ?
Vous savez certainement que plus les accélérateurs de particules sont grands, plus ils sont puissants et permettent d’atteindre des énergies de collision élevées. Pour savoir si on risque de créer un trou noir au CERN, il faut se demander si l’énergie atteinte par le collisionneur LHC est suffisamment grande pour faire naître un trou noir. Mais plus les trous noirs sont lourds, plus il faut d’énergie pour les faire apparaître, donc ce qu’on a besoin de savoir, c’est l’énergie qu’il faut pour créer le plus petit trou noir possible.
Le « hic », c’est que de manière détaillée, on ne sait pas vraiment ce qu’est le plus petit trou noir possible. Pour cela il faudrait qu’on dispose d’une théorie capable de correctement décrire les trous noirs microscopiques, or nous n’en avons pas ! Et pourtant nous ne sommes pas démunis, car on peut estimer l’ordre de grandeur de cette énergie minimale de création de trou noir : il suffit d’utiliser l’analyse dimensionnelle !
L’analyse dimensionnelle (qui manifestement se trouve heureusement au programme de physique du lycée), c’est ce qui dit en gros que dans une formule, il faut que le résultat ait la bonne unité de mesure (on recommande souvent aux élèves de vérifier l’homogénéité de leur formule). Il se trouve que dans certaines situations, en appliquant ce principe on peut retrouver de bons ordres de grandeur des quantités qu’on cherche, sans faire de calcul détaillé et simplement en considérant le fait que les unités doivent coller.
Voyons ici comment se principe permet d’estimer l’énergie minimale qu’il faut pour créer un trou noir, ce qu’on appelle l’énergie de Planck.
L’énergie de Planck
On sait qu’il existe 3 constantes fondamentales régissant la physique théorique : la vitesse de la lumière \(c\), la constante de Planck \(\hbar\), et la constante de gravitation universelle \(G_0\). Voici ci-dessous la valeur de chacune de ces constantes avec la bonne unité :
Vitesse de la lumière : \(c=3.10^8\ m/s\)
Constance de Planck \(\hbar =10^{-34}\ m^2.kg/s\)
Constante de Newton \(G_0 = 6.10^{-11}\ m^3/kg/s^2\)
Et maintenant, avec ces trois constantes, fabriquez moi une quantité qui soit une énergie ! Petit indice, une énergie, ça a pour unité le Joule, or 1 Joule, ça n’est autre que \(1\ kg.m^2/s^2\).
En cherchant un peu, vous allez vous rendre compte qu’il n’existe qu’une seule manière de fabriquer une énergie avec les 3 constantes fondamentales, c’est de faire la combinaison suivante :
\(E_P=\sqrt{\frac{\hbar c^5}{G_0}}\)
Cette quantité, que j’ai noté \(E_P\) s’appelle l’énergie de Planck, et donne l’ordre de grandeur de l’énergie qu’il faudrait pour créer le plus petit trou noir possible. Je vous fait grâce de l’application numérique, mais on trouve en gros une énergie de \(10^9\) joules. Une fois convertie en téra-électrons-volts (TeV), l’unité favorite des accélérateurs de particule, on trouve environ \(10^{16}\) TeV.
Pour créer un micro trou noir, il nous faut donc une énergie d’environ \(10^{16}\) TeV. Sachant que le nouveau collisionneur LHC est susceptible d’atteindre au mieux des énergies d’environ 7 TeV, on comprend qu’a priori, on est loin…très loin…de pouvoir y créer le moindre trou noir ! Donc pas de risque a priori…sauf si on fait intervenir des dimensions supplémentaires !
Une gravité pas si faible
Vous le savez certainement, les dimensions supplémentaires ont le vent en poupe en physique théorique, en particulier dans les différentes versions de la célébrissime théorie des cordes dont je parlais dans ce billet.
Or il se trouve que la présence de dimensions supplémentaires pourrait modifier le calcul de l’énergie de Planck que je présentais ci-dessus. En effet si l’énergie de Planck est si grande, c’est notamment parce que la constante de gravitation \(G_0\) est très petite, ce qui traduit le fait que la force de gravité est très faible, comparativement aux autres forces comme l’électromagnétisme.
Maintenant imaginons que l’on vive dans un monde avec plein de dimensions supplémentaires, que la gravité y soit en réalité une force assez forte, mais qu’elle nous apparaisse faible car elle se trouve « diluée » dans les dimensions supplémentaires. Cela voudrait dire que la véritable constante G à prendre dans le calcul pourrait être plus élevée que prévue, et donc l’énergie de Planck plus basse !
Mais pour calculer ça dans le détail, il faut reprendre notre analyse dimensionnelle.
L’énergie de Planck en 3+n dimensions
Alors allons-y : supposons qu’il y ait n dimensions d’espace supplémentaires, en plus des 3 que nous connaissons bien. La première modification qu’il faut considérer, c’est celle de la loi de gravité de Newton. En 3 dimensions, le potentiel de gravité associé à l’attraction de 2 corps situés à distance \(r\) s’écrit
\(V(r) = – \frac{G_0 m_1m_2}{r}\)
Cette forme du potentiel obéit à une propriété particulière : la loi de Gauss, qui affirme que le flux du champ gravitationnel à travers une surface est égal à la masse enfermée par cette surface (programme de lycée scientifique aussi, non ?)
Si maintenant on se place en (3+n) dimensions, il faut modifier l’expression du potentiel pour que la loi de Gauss soit toujours satisfaite, car maintenant les surfaces et les volumes ont \(n\) dimensions de plus. La forme qui colle est la suivante :
\(V(r) = – \frac{G_n m_1m_2}{r^{1+n}}\)
où \(G_n\) désigne la constante de gravitation en (3+n) dimensions. Comme vous pouvez le voir en regardant attentivement les unités dans cette formule, cette hypothétique constante ne s’exprime pas dans la même unité que celle que l’on connait. La bonne unité, c’est le \(m^{3+n}/kg/s^2\).
Donc pour fabriquer une énergie à partir de \(G_n\), de \(\hbar\) et de \(c\), il faut modifier le calcul d’analyse dimensionnelle. Le calcul n’a rien de compliqué, je vous l’épargne, voici comment fabriquer l’énergie de Planck en 3+n dimensions à partir des 3 constantes :
\(E_P = \left(\frac{h^{1+n}c^{5+n}}{G_n}\right)^{\frac{1}{2+n}}\)
Donc si l’hypothèse des dimensions supplémentaires est correcte, on peut calculer la véritable énergie de Planck en 3+n dimensions…à condition de connaitre la valeur de \(G_n\) !
Et Gn, ça vaut combien ?
Pour deviner \(G_n\), on va partir de ce qu’on connait, à savoir la valeur \(G_0\) que l’on observe dans notre monde apparemment tridimensionnel. Comme je l’expliquais, l’idée sous-jacente est que ce qu’on observe, c’est une version diluée de la gravité à cause des dimensions supplémentaires. Alors essayons de comprendre la manière dont \(G_n\) se dilue pour donner \(G_0\).
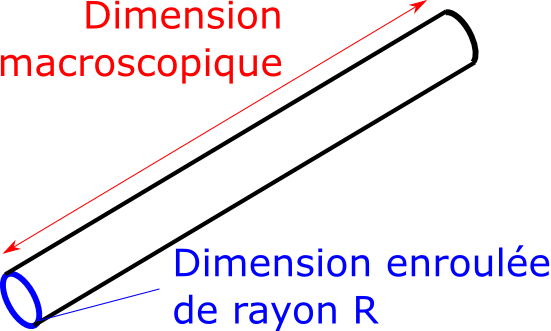 Pour calculer l’effet de la dilution, on va supposer conformément aux habitudes que les dimensions supplémentaires sont des dimensions « enroulées », qui sont compactées selon un rayon R, comme sur le dessin ci-contre. On peut alors partir de l’expression du potentiel de gravité en (3+n) dimensions, et en déduire le potentiel « apparent » vus des 3 dimensions macroscopiques (non-enroulées) qui nous sont familières. On a
Pour calculer l’effet de la dilution, on va supposer conformément aux habitudes que les dimensions supplémentaires sont des dimensions « enroulées », qui sont compactées selon un rayon R, comme sur le dessin ci-contre. On peut alors partir de l’expression du potentiel de gravité en (3+n) dimensions, et en déduire le potentiel « apparent » vus des 3 dimensions macroscopiques (non-enroulées) qui nous sont familières. On a
\(V(r) = -\frac{G_n m_1 m_2}{r^{1+n}}\approx -\frac{G_n m_1 m_2}{R^n r}\)
On voit bien dans cette formule qu’on retrouve notre potentiel de gravité habituel, pour peu que notre constante \(G_0\) s’identifie au rapport \(G_n/R^n\). Donc connaissant \(G_0\), on peut retrouver \(G_n\) en faisant une hypothèse sur le rayon \(R\), et bien sûr sur le nombre \(n\) de dimensions supplémentaires.
Alors, alors ? On va en voir, des trous noirs ?
Si je replace l’expression de \(G_n\) par \(G_0 R^n\) dans la formule de l’énergie de Planck en 3+n dimensions, j’obtiens :
\(E_P = \left[\left(\frac{\hbar c}{R}\right)^n \frac{\hbar c^5}{G_0}\right]^{\frac{1}{2+n}}\)
Voici différentes applications numériques de ce calcul pour plusieurs choix de n et de R :
- Pour n=2 et un rayon R de 10 microns, l’énergie de Planck descend à 3 TeV;
- Pour n=3 et un rayon R de 10 nanomètres, l’énergie de Planck est d’environ 1 TeV;
- Pour n=6 et un rayon R de 0.01 picomètres, l’énergie de Planck est d’environ 1.5 TeV;
Comme vous le voyez, les dimensions supplémentaires peuvent considérablement abaisser l’énergie de Planck, jusqu’à des valeurs de l’ordre des puissances atteintes au LHC. Donc avec des dimensions supplémentaires qui diluent la gravité, il serait parfaitement envisageable de créer des micro-trous noirs lors des expériences du LHC !
Mais rassurez vous, puisque les énergies atteintes au CERN sont comparables à celles de nombreux rayons cosmiques qui atteignent la Terre quotidiennement, si nous devions disparaître en étant avalés par un trou noir, ça fait longtemps que ce phénomène se serait produit !
Voilà, j’espère que vous avez pu apprécier la beauté de l’analyse dimensionnelle, qui à partir de considérations assez génériques nous permet d’approcher les conséquences des théories fondamentales les plus audacieuses !
Pour aller plus loin
Dans ces calculs, vous pouvez probablement être surpris par la grande taille des dimensions supplémentaires (peut être de l’ordre du micron ?). Si elles étaient si grosses, est-ce qu’on aurait pas déjà dû les voir ? Mais rappelez vous que dans notre hypothèse, seule la gravité est capable de se propager dans les dimensions supplémentaires. Or la gravité est une force qu’on ne connait à peine en dessous du millimètre ! Les curieux peuvent aller jeter un oeil aux manips de Hoyle pour tester la force de gravité aux échelles inférieures à 100 microns. En gros s’il existe des dimensions supplémentaires, on s’attend à ce que dans ces manips la force de gravité se mette à dévier de sa loi en \(1/r^2\) quand on passe à des échelles inférieures à la taille caractéristique des dimensions enroulées, pour devenir une force en \(1/r^{(n+2)}\), conformément au potentiel que j’écrivais plus haut.
Autre considération : si on crée effectivement des trous noirs au LHC, est-ce qu’on ne devrait pas s’en rendre compte ? D’après les théoriciens, un trou noir de petite taille devrait rapidement s’évaporer (selon le principe du rayonnement de Hawking), et laisser derrière lui une signature bien reconnaissable (du genre rayonnement de corps noir). A ce stade on a rien vu de tel : donc soit on ne crée pas de trous noirs, soit en quantité trop faible pour qu’ils soient détectés.


48 Comments
Bel article, avec de jolis calculs comme on les aime !
Pour ceux qui se posent encore des questions et qui aime plus les bandes dessinées que les livres de maths, il peuvent toujours se tourner vers la BD du LHC sur le sujet : http://www.lhc-france.fr/spip.php?article180#mai09
J’ai un peu de mal à comprendre cet enthousiasme pour l’analyse dimensionnelle. Pour retrouver un résultat, pourquoi pas. Mais pour en établir un… Quels sont les arguments indiquant qu’il n’y a pas une très grosse constante multiplicative par exemple ?
Il n’y a effectivement absolument aucun argument qui donne la valeur de la constante multiplicative, et qui donc permette d’exclure une très grosse constante.
Néanmoins, il ne faut pas oublier que l’on parle ici d’ordre de grandeur avec des différences très violentes, d’un facteur 10^16 quand même ! Donc même s’il y a une (improbable) grosse constante, la différence reste quand même très très significative. En tout cas bien supérieur à l’impact du nombre de dimensions ou du rayon de compactification dans le calcul !
Même si le rapport est 10^16, la constante multiplicative peut a priori être 10^100.
Je comprend bien l’utilité pour retrouver rapidement le résultat dans un cas où on sait que ça marche. Je comprend également l’utilité pour imaginer la tête du résultat et être ainsi guidé dans ses calculs. Mais l’utilisation que tu sembles en donner me paraît vraiment être non scientifique. Vu de l’extérieur j’ai plutôt l’impression que l’on est dans le domaine de la croyance. Je me trompe ?
Brr… Je frissonne à l’idée que certaines personnes puissent trouver cela convaincant, mais c’est peut-être mon côté matheux qui parle 🙂
J’ai oublié de te remercier pour ta réponse : merci !
C’est bien un raisonnement de matheux, ça 🙂
Je te rassure, le raisonnement qui consiste à estimer des ordres de grandeur par analyse dimensionnelle est tout à fait valable pour un physicien. Je ne connais absolument aucun cas où la constante sans dimension est 10^100, ni même beaucoup plus que 10^6. On obtient rarement des choses très différentes de quelques facteurs simples et quelques puissances de \pi.
L’exemple le plus exotique que je connaisse : la divergence dans la correction à deux boucles pour la matrice S en quantification perturbative de la relativité générale (ouf !) où le préfacteur est
209/(737280 \pi^4)
cf Goroff & Sagnotti « The ultraviolet behavior of Einstein gravity », nuclear physics B 266 (1986)
Mais puisque tu me pousses dans mes retranchements, je vais être obligé de dégainer un raisonnement un peu plus convaincant, mais que j’ai soigneusement évité initialement pour ne pas plomber le billet 🙂
Alors allons-y, pour cela on va faire un peu de gravité quantique avec les mains :
* Pour créer un trou noir de masse M, il faut arriver à confiner cette masse M à l’intérieur d’une boule de rayon inférieur à R = 2 G.M / c^2, ce qu’on appelle le rayon de Schwarzchild (résultat de la relativité générale d’Einstein).
* D’un autre côté, l’incertitude d’Heisenberg de la mécanique quantique nous enseigne qu’une particule de masse M ne peut être localisée sur une longueur inférieur à sa longueur d’onde de Compton, laquelle vaut h.c/M
Si tu combines ces deux résultats, tu vois que la masse minimum à atteindre pour que la longueur d’onde de Compton soit inférieure au rayon de Schwarzschild (et donc créer un trou noir), c’est d’avoir
M² > hc/2G.
Si je convertit cette contrainte sur la masse en une contrainte en énergie, car E=Mc², je trouve
E > \sqrt{hc^5/2G}
On retrouve notre relation, à quelques facteurs pi et racine(2) totalement négligeables 🙂
C’est parfaitement ok pour un matheux, tu as juste mis un prior sur la taille de la constante… 🙂
Oh tiens, ça faisait longtemps que je n’avais lu un article sur les mini trous noirs du LHC, cool =) !
> Donc avec des dimensions supplémentaires qui diluent la gravité, il serait parfaitement envisageable de créer des micro-trous noirs lors des expériences du LHC !
> D’après les théoriciens, un trou noir de petite taille devrait rapidement s’évaporer (selon le principe du rayonnement de Hawking), et laisser derrière lui une signature bien reconnaissable (du genre rayonnement de corps noir).
J’ajouterai que l’analyse de la signature de l’évaporation permet en outre de déduire le nombre de dimensions supplémentaires, sujet de pré-thèse(*) d’un de mes camarades de promo’ en Master 2, sous la direction de notre prof de cosmologie, lequel est justement l’un des principaux experts français sur les mini trous noirs (voir son interview sur le sujet, à l’époque de la polémique sur la « destruction de la Terre par le LHC » : http://www.futura-sciences.com/fr/news/t/physique-1/d/les-mini-trous-noirs-au-lhc-une-interview-daurelien-barrau_16425/ ).
(*) Bon finalement, il a fait sa thèse sur la recherche de Z’->e+e- dans ATLAS.
> Mais rassurez vous, puisque les énergies atteintes au CERN sont comparables à celles de nombreux rayons cosmiques qui atteignent la Terre quotidiennement, si nous devions disparaître en étant avalés par un trou noir, ça fait longtemps que ce phénomène se serait produit !
Je me permettrai de justifier cette affirmation de manière chiffrée, en copiant-collant un bout de texte que j’avais rédigé quelques semaines après l’interview susmentionnée et dans lequel je reprends les chiffres de mon prof mais à « échelle humaine » (jours et km² au lieu de s et cm²), en ajoutant une info quant à la dangerosité des mini trous noirs :
Pour le « trou noir avaleur de la Terre », je confirme qu’il n’y a aucun danger, par une observation expérimentale simple : sur **chaque km²** de la surface de la Terre, les rayons cosmiques produisent **chaque jour** en moyenne 4.3 collisions plus énergétiques (jusqu’à 1000× plus) que ce que fait le LHC si on le pousse à fond.
Multipliez par la surface de la Terre (~500 millions de km²) et par le temps qu’elle existe (~1600 milliards de jours), et vous aurez une idée du nombre de fois que la Terre a déjà « failli être engloutie par un trou noir » #tritop#.
Pour info, le temps d’évaporation d’un trou noir (pendant lequel il risque d’absorber quelque chose et de grossir) est proportionnel au cube de sa masse, donc les collisions de rayons cosmiques mesurées jusqu’à 1000× plus énergétiques que dans le LHC donnent potentiellement des trous noirs qui mettent 1 milliard de fois plus de temps à s’évaporer, et qui sont donc 1 milliard de fois plus dangereux que ce que l’on sera capable de faire au LHC.
Et pourtant, la Terre est toujours là :o…
Super article, bravo. Le fait qu’on n’ait pas observé de trous noirs microscopiques signifie-t-il du coup qu’il n’y a pas d’autres dimensions? Qu’elles sont trop petites? Que la gravité ne s’y dilue pas? Ou bien … Rien du tout?
Comme souvent, le fait de ne rien observer permet d’exclure certains scénarios…mais en laisse beaucoup d’autre ouverts !
De plus le raisonnement tenu ici fixe une échelle d’énergie, mais ne nous dit rien sur le taux de production de trous noirs. Ca se trouve le taux est si faible qu’un seul trou noir sera produit dans toute l’exploitation du LHC, et qu’on ne s’en rendra pas compte !
Bonjours !
Par contre le rayonnement de Hawking se produit une foie le trou noir formée, se n’est pas l’étape 1 de la formation d’une singularité.
Comme les paramètres de la formation d’une singularité qui anime les trou noir ne nous est pas connue, ihihi… plus il y a de masse d’Haddron en colision, plus la vue d’enssemble nous seras dévoiler, a commencer par le fameux Higgs.
Comme il existe plusieur sorte de mécanique de trou noir, la chose a ne pas produire dans une colisioneur serais de déclancher une réaction en chaine au niveau d’un intriquement a large rayon.
Vous ZZZz’…. inquitez pas, on est vraiment loin de la.
Cats
Pingback: Des rayons cosmiques très énergétiques ! … trop énergétiques ? « Science étonnante
Pingback: À propos des hypothétiques mini-trous noirs du LHC « jpcmanson
bonjour
LE TROU NOIRE A UNE RACINE
LE TROU NOIRE VISBLE SUR UN ANGELE DE VISION
LE TROU EST DU A UNE SUPERE POSITION DES SERCLE LUMINEUX LEURS LUMIERE REFLICHI CREE UNE TURBULANSE ET REMANTE LE TROU ON GARDANT SA RACINE LE TROU OU LE PIRIMAITRE DE CE DERNIER DEVIENT LUMINEUX………………!
Bonjour
Le rayonnement de Hawking est il valable a l’interieur de notre atmosphère?
A priori oui, pas de limitation due à la présence de l’atmosphère. En revanche, il est important de rappeler que ce rayonnement n’est pour l’instant qu’une construction théorique ! Personne ne l’a jamais vu…encore que, il y a quelques manips dont il faudra que je parle un jour !
Merci pour cette réponse,il n’en reste pas moins que les scientifiques du CERN jouent avec la matière en sachant que le risque zéro n’existe pas alors la véritable question a se poser est de savoir si la connaissance nous donne le droit de tout expérimenter au détriment de l’impact sur l’humanité.
De plus si l’accélérateur subit un incident grave tel la formation d’un trou noir ne se résorbant pas ou pire encore (il y a aussi le fameux problème des quarks et de la matière étrange pour les connaisseurs) personne ne pourra assigner personne,les cris d’horreur et les larmes laisseront place au silence glacial des stèles désertées.
Notre humanité n’a pas de prix et certainement pas celui de la connaissance aussi importante soit elle.
je suis juste complètement d’accord avec Nibiru !!! l’être humain aussi intelligent qu’il soit ne maîtrisera pas l’univers. Vous les scientifiques du CERN redescendez sur terre …. nous n’avons pas besoin de vous pour détruire la planète, on mettra juste un peu plus de temps et nous finirons par prendre conscience de nos erreurs.
j’espère seulement qu’ils savent ce qu’ils font au CERN…
bonjour, je voulai vous demander, sachant que la possibilté d’univers, parradoxallement ne pouvont nous pas essayer d’envoyer un objet de matiere trés simple permetant juste d’evalué la matiere directe d’un trou noir (ou bleu )a partir d’un planette mieux placer exemple(mars)meme avec la distance grace a la puissance antigravitationnelle(pas si faible comme vous l’avez dit )nous pourion utiliser un faiseau permettant cela non ? cela couterai des miliard d’euro mais cela pourra resoudre les problèmes de
-transport (grace a l’anti graviter permetant grace a un trou noir(portable de s’attirer a l’endroit desiré)
-de matiere(grace a se systeme nous pourrion aller chercher la matiere la ou elle se trouve en grande cantiter et ou elle se repproduit vite)
-et donc de crise (meme en investissant cher nous n’aurrions plus de probleme de matiere de transport et d’espace donc plus besoin d’argent)
ceci ne son que des calculs realiser en 40minutes peu probable qu’il soit realisable mai qui ne tente rien na rien
PS:dsl pour les faute je voulais écrire vite car j’ai un cour de phisique a donner.
🤦♂️
j’ai refait mes calculs en esayant d eles produire l’energie a maitriser serai trop grande et detrurai grosso modo tout un continents.
mieux vos ne pas courir se risque
Slt, thekail je ne peux répondre a ta question je suis juste un curieux sans aucune connaissance mais je pense que ScienceEtonnante ou quelqu’un d’autres sur ce forum peuvent te donner un réponse à tes questions…
Pingback: LE CERN | Pearltrees
Pingback: Que se passe-t-il quand on tombe dans un trou noir ? (ou le problème du firewall) | Science étonnante
je voudrai contacter le cern pour voyager dans le temps et changer le passé car le présent me fait souffrir et j’aurai pu éviter ceratines situations
🤦♂️
Pingback: Comment estimer la puissance d’une bombe atomique à partir d’une photo ? | Science étonnante
les avantages des trous noirs de notre galaxie peut on les citer ?
La vie !
Et oui, sans trou noir, pas de quasar, sans quasar pas de galaxie, sans galaxie pas de planète !
Sa vous va comme avantage ?
Pingback: Pourquoi est-il impossible de se sortir d’un trou noir ? (2/2) | Science étonnante
Pingback: La théorie des cordes | Science étonnante
Début 2013, le LHC a été fermé pour augmenter son énergie de collision à 13 TeV (téraélectronvolts) — 6,5 TeV dans chacun des deux faisceaux qui tournent en sens inverse dans l’anneau.
«Treize TeV constitue un nouveau record, qui va ouvrir la voie, espérons-le, à une nouvelle physique», déclare Mirko Pojer, opérateur au centre de contrôle du CERN.
L’énergie maximale atteinte jusque-là par le LHC avait été de 8 TeV en 2012. Le LHC pourra monter jusqu’à un maximum de 14 TeV.
Amateur de sciences, je m’intéresse à ces questions tout en ayant un bagage scientifique assez faible (terminale S).
Y a t-il des discussions dans le milieu scientifique pour savoir jusqu’à quelle énergie on va s’autoriser à monter avec des collisionneurs de particules?
Merci
En fait, si on fabrique un trou noir de cette taille un jour, il va s’évaporer en un temps beaucoup trop court pourque ce soit un réel danger pour nous. Donc rien à craindre (voir « évaporation des trou noir » ou « rayonnement de hawkins »)
Je pense que l’homme joue avec le feux avec ce genre manipulation. Les physiciens sont parvenus a extraire de l’énergie des atomes, ils arriverons un jour à fabriquer un trou noir. C’est évident. Le LHC, c’est un peu comme mettre une mitraillette entre les mains d’un singe…
Les scientifiques du CERN sont entrains d’ouvrir une ou des portes dans d’autre dimensions. Ces portes ont été volontairement fermer pour notre bien à tous, ces scientifiques croient qu’ils vont faire de nouvelle connaissance technologique, en fait ils vont libérer des milliers de démon sur la terre, ces anges déchus ont été enchainé pendant plusieurs milliers d’année, à cause d’eux nous courront à la catastrophe Dans .Jude 1.6 : « […]qu’il a réservé pour le jugement du grand jour, enchaînés éternellement par les ténèbres, les anges qui n’ont pas gardé leur dignité, mais qui ont abandonné leurs propres demeurent. ».qui n’ont pas gardé leur dignité, mais qui ont abandonné leur propre demeure. ».
Comment un esprit aussi irrationnel que le vôtre peut il exister ? Quand avez vous perdu tout esprit critique ?
Article sympas. je viens de lire un article sur slate.fr « L’accélérateur de particules de Genève va révéler des univers parallèles » et j’ai compris grâce a vous ce qu’il voulait dire… merci
Je crois avoir découvert une petite imperfection dans cet article : dans la partie « L’énergie de Planck », la lettre utilisée est ħ, qui désigne habituellement la constante de Dirac (h/2π), et non la constante de Planck (oui, j’adore dire à un prof qu’il a fait une erreur pendant son cour :3); A part ça, c’est un super article qui donne un super exemple de l’utilisation de analyse dimensionnelle (autre que la mémorisation des formules)
Mais encore la dissolution de la gravité n’est qu’une simple hypothèse et non un fait ! ET si, et je dis bien si, la gravité ne serait pas constante ou plutôt plus élevées dans les autres dimensions que dans la notre quels en serait les « conséquences » ?
Pingback: La Théorie des Cordes — Science étonnante #5 – LightX
Pingback: La Théorie des Cordes — Science étonnante #5 - Blog NSellier TV
J’ai mis au moins une heure à trouver
sqrt (C^5.h/Go) mais ça en valait la peine ! Je suis fier de moi XD
Bonjour et merci pour votre blog.
Votre conclusion :
« Donc avec des dimensions supplémentaires qui diluent la gravité, il serait parfaitement envisageable de créer des micro-trous noirs lors des expériences du LHC !
Mais rassurez vous, puisque les énergies atteintes au CERN sont comparables à celles de nombreux rayons cosmiques qui atteignent la Terre quotidiennement, si nous devions disparaître en étant avalés par un trou noir, ça fait longtemps que ce phénomène se serait produit ! »
ne remet elle pas en cause la théorie des cordes dans ce cas ?
Pingback: La Théorie des Cordes — Science étonnante #5 | JetBip
Quand on nous parle d’Albert et Luis (les 2 astronautes qui sont à proximité d’un trou noir, si Albert va à l’horizon des événements et se retourne juste avant, alors « il voit en un instant toute l’histoire future de l’univers » donc très logiquement,
si Luis indécis décide au bout de 10 ans de le rejoindre, Albert va voir Luis arriver derrière lui (Luis fait partie de l’histoire future de l’Univers, c’est incontestable donc si dans ce futur de l’univers Luis vient à l’horizon alors Albert va le voir derrière lui
et tout proche, ils vont même pouvoir se parler sauf que Luis est 10 ans plus vieux).
Et si on applique ça à tout ce qui arrive ou est arrivé à l’horizon des événements, alors cela signifie qu’au final, tout le monde va y entrer mais en même temps au moment où l’univers disparaîtra !!!!
Tout ça pour dire qu’il est impossible de revenir d’un trou Noir car tout simplement si tu y es entré, c’est que l’Univers d’où tu viens n’existe plus
(j’ai l’impression d’être un illuminé à force d’essayer de comprendre. D’ailleurs ceux à qui j’explique cela me prennent pour un fou…)
Pingback: La Théorie des Cordes — Science étonnante #5 – MovieCS