 On a souvent tendance à penser qu’il a fallu attendre la Renaissance pour que l’humanité découvre que la Terre n’était pas plate. C’est une fausse croyance, car l’idée que la Terre soit ronde date de l’Antiquité, et était partagée par de nombreux savants comme Platon ou Aristote.
On a souvent tendance à penser qu’il a fallu attendre la Renaissance pour que l’humanité découvre que la Terre n’était pas plate. C’est une fausse croyance, car l’idée que la Terre soit ronde date de l’Antiquité, et était partagée par de nombreux savants comme Platon ou Aristote.
D’ailleurs en 200 avant J.C., Eratosthène a même réussi l’exploit de calculer la circonférence de la Terre à quelques centaines de kilomètres près, puisqu’il l’estima à 39 375 km, alors que la valeur actuellement admise est autour de 40 070 km !
Voyons ensemble comment il a procédé.
Le soleil au fond des puits
A la fin du IIIème siècle en Egypte, sous le règne du pharaon Ptolémée III, le grec Erathostène était un savant réputé. Il dirigeait notamment la grande Bibliothèque d’Alexandrie, et fut le précepteur du futur pharaon Ptolémée IV.
 Fort de ses connaissances d’astronomie et de géographie, il mis au point une méthode purement géométrique pour estimer la circonférence de la Terre. Pour cela, il partit de la constatation suivante : « Dans la ville de Syène, à midi le jour du solstice d’été, le soleil éclaire le fond des puits ».
Fort de ses connaissances d’astronomie et de géographie, il mis au point une méthode purement géométrique pour estimer la circonférence de la Terre. Pour cela, il partit de la constatation suivante : « Dans la ville de Syène, à midi le jour du solstice d’été, le soleil éclaire le fond des puits ».
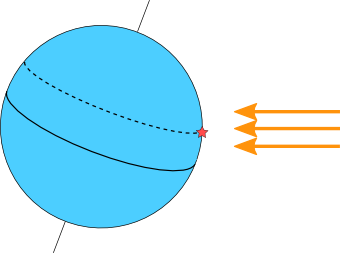
Que signifie cette phrase énigmatique ? Tout simplement qu’à Syène, le 21 juin à midi, le soleil est exactement à la verticale du sol (et que ses rayons peuvent donc atteindre le fond des puits.)
Du point de vue géographique, avoir le Soleil à la verticale au solstice d’été signifie que l’on se trouve sur le tropique du Cancer. C’est ce qu’illustre la figure ci-contre, qui rappelle l’inclinaison de l’axe de rotation de la Terre, et montre la position de Syène, située sur le lieu de l’actuelle ville d’Assouan, non loin du tropique.
 A l’ombre du phare
A l’ombre du phare
Si le 21 juin à Syène, le Soleil est à la verticale du sol, c’est que la trajectoire de ses rayons à cet endroit passe par le centre de la Terre. Pour déterminer la circonférence de la Terre, Erathostène a alors réalisé une deuxième mesure.
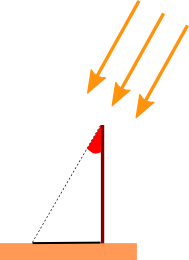
Le 21 juin, mais cette fois à Alexandrie, il observa l’ombre du Phare, et mesura l’angle qu’elle formait avec son sommet (bon, pour certains, il ne s’agissait pas de l’ombre du Phare d’Alexandrie, mais de celle d’un simple morceau de bois).
Que ce soit un phare ou un bout de bois, le résultat est le même, Eratosthène observa que l’angle formé valait 1/50ème de cercle, soit 360°/50 = 7.2°. C’est ce qu’illustre le dessin ci-contre, dont j’ai exagéré l’angle pour que ce soit plus facile à visualiser.
Après avoir mesuré cet angle, Eratosthène fit ce qu’aurait fait tout bon élève de 5ème, il fit une figure et invoqua un théorème de géométrie.
La figure ci-dessous montre la surface de la Terre, et la manière dont les rayons du Soleil viennent la frapper le 21 juin à Syène (point A) et à Alexandrie (point B). D’après le théorème des angles alternes-internes, les deux angles en rouge sur la figure sont égaux.
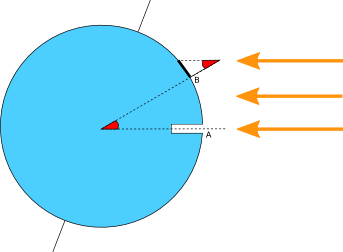 L’angle au sommet du phare est donc égal à l’angle qui sépare les deux villes à la surface de la Terre. D’ailleurs le 7.2° que nous avons trouvé correspond à peu près à leur différence de latitude (31°12′ et 24°05′).
L’angle au sommet du phare est donc égal à l’angle qui sépare les deux villes à la surface de la Terre. D’ailleurs le 7.2° que nous avons trouvé correspond à peu près à leur différence de latitude (31°12′ et 24°05′).
Puisque la mesure de cet angle par Erathostène à Alexandrie donne 1/50ème de cercle, la distance entre Syène et Alexandrie vaut 1/50ème de la circonférence de la Terre. Et pour calculer celle-ci, il ne nous reste plus qu’à connaître la distance de Syène à Alexandrie…et c’est là que le chameau entre en jeu.
A dos de chameau
Pour mesurer les distances, on sait qu’un chameau met environ 50 jours pour aller d’Alexandrie à Syène, et qu’en un jour il parcours une distance de 100 stades (le stade étant l’unité de distance en vigueur à ce moment là). La distance entre les deux villes est donc d’environ 5000 stades. Et puisque cette distance vaut 1/50ème de la circonférence de la Terre, c’est que cette dernière mesure environ 250 000 stades.
Euh, mais ça vaut combien un stade ? Apparemment, chez les Egyptiens, le stade valait 157.5 mètres. Ce qui nous donne comme estimation de la circonférence de la Terre 39 375 km. Pas mal quand on sait que la véritable valeur est environ de 40 000km !
Quelques éléments sur la validité de la mesure
Le calcul fait par Erathostène repose sur quelques suppositions que l’on peut mentionner et discuter.
 La première, c’est bien sûr que la Terre est ronde ! Or on sait aujourd’hui qu’il s’agit plutôt d’une sphère légèrement applatie au niveau des pôles. Ce qui fait que la circonférence de l’équateur mesure environ 70km de plus que la circonférence qui passe par les pôles.
La première, c’est bien sûr que la Terre est ronde ! Or on sait aujourd’hui qu’il s’agit plutôt d’une sphère légèrement applatie au niveau des pôles. Ce qui fait que la circonférence de l’équateur mesure environ 70km de plus que la circonférence qui passe par les pôles.
La deuxième supposition, c’est que les rayons du Soleil qui frappent la Terre sont bien parallèles entre eux. Cela revient à supposer que le Soleil est situé suffisament loin, ce qui en l’espèce est une approximation tout à fait raisonnable.
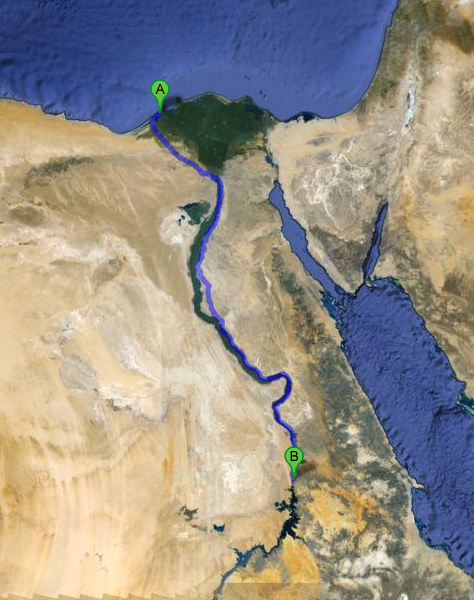
Enfin la dernière hypothèse faite par Eratosthène, c’est que Syène et Alexandrie sont situées sur le même méridien. C’est en effet une supposition implicite quand on réalise la figure qui nous a permis de conclure. Bien que les deux villes soient toutes les deux situées sur le cours du Nil, elle ne sont pas strictement sur le même médirien, comme le montre la carte ci-contre. Heureusement, Eratosthène commis une autre erreur qui compensa celle-ci : par la technique du chameau il sous-estima légèrement la distance entre les deux villes (il devait avoir des chameaux de compétition…)
A vous de jouer !
 Pour reproduire le calcul d’Eratosthène, nul besoin d’aller en Egypte, ni d’attendre le solstice d’été pour s’y balader à dos de chameau. On peut utiliser deux villes quelconques, du moment qu’elle sont bien situées sur le même méridien. Pour cela il faut adapter un peu la mesure.
Pour reproduire le calcul d’Eratosthène, nul besoin d’aller en Egypte, ni d’attendre le solstice d’été pour s’y balader à dos de chameau. On peut utiliser deux villes quelconques, du moment qu’elle sont bien situées sur le même méridien. Pour cela il faut adapter un peu la mesure.
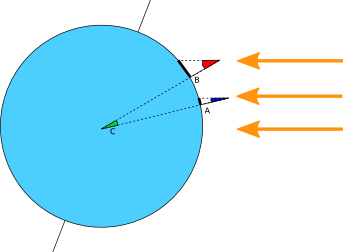
Supposons que vous viviez à Nancy, et que vous ayez un ami habitant Toulon. Le même jour, à midi au soleil, plantez un bâton bien vertical dans le sol, repérez l’ombre formée et mesurez chacun l’angle au sommet. Avec un tout petit peu de géométrie du triangle (voir ci-contre), vous pouvez vous convaincre que l’angle C est la différence entre l’angle B à Nancy et l’angle A à Toulon.
Il ne vous reste plus qu’à connaître la distance entre Nancy et Toulon, et vous retrouvez la circonférence de la Terre ! Bien sûr dans ce calcul, il y a aussi une hypothèse forte, celle qu’on puisse trouver du soleil à Nancy…


126 Comments
Pingback: La mesure de la circonférence de la Terre par Eratosthène | Beyond the cave wall | Scoop.it
aidez moi j’arrive pas a calculer
bah prends ta calculette mdr on est pas ton esclave…
Nan mais serieux tu te prends pour qui a jouer les caïds???
tu m’degoute….t’es pauvres… tu t’habille chez gemo a tout les coups…
tu te rends compte de ce que tu dit??? franchement parler de ca alors qu’en République Démocratique du congo, Eddy-malou dit des trucs tres interessant sur le congolexicomatisation des lois du marché…
tentacules.
Cubiquement,
Niellow alias MOMO2.0
Bravo ! Tout est clair. Ce sont des notions que nous aurions dû avoir au collège en 1956. J’ai pris un grand plaisir à vous lire. Merci beaucoup. L’apprentissage des mathématiques aurait paru un peu moins austère.
Quelqu’un peut m’expliquer le calcul parce que je n’ai pas compris .
(360°/D°) X N km = à peu près la circonférence de la Terre
D° est la différence des angles des deux bâtons à midi
N km est la distance en km ou stades qui sépare les deux bâtons
il faut se trouver sur le même méridien
exemple D° = 9° et N km = 100 km alors (360°/9°) X 100 km = 40 X 100 km = 4000 km
Je pense que l’on peut rajouter une hypothèse à ta liste, qui est évoquée implicitement dans l’article : la distance est basée sur une distance journalière parcourue par le chameau à la fois constante et bien connue (100 stades).
Mais la température, la fatigue du chameau, la qualité de la route peuvent être autant de facteurs rendant cette distance journalière variable, et j’imagine que les 100 stades et les 50 jours sont plus un ordre de grandeur qu’une estimation précise. On devrait donc s’attendre à une marge d’erreur sur la distance assez forte, typiquement 20%.
La bonne précision évoquée relève donc à mon sens du coup de bol. A moins que la méthode de mesure de la distance soit différente (la mesure de la longitude n’a été résolue complètement qu’au XVIIIe siècle par les Britanniques).
Tu as parfaitement raison, c’est cet effet que je mentionne à la fin en disant que les erreurs de distance et de longitude se compensent.
D’après la fonction de mesure de distance à vol d’oiseau de Google Maps, la distance entre Alexandrie et Assouan est de 842 kilomètres, soit 5346 stades. Le coup de bol d’Eratosthène, c’est que les deux villes ne sont pas sur le même méridien, mais que cette sous-estimation de la distance lui a permis de retomber quand même sur la bonne valeur.
Ca n’enlève rien à l’exploit, même s’il s’était trompé de 10000 kilomètres sur les 40000 km, j’aurai considéré ça comme une mesure vachement précise pour l’époque ! (encore qu’apparemment Aristote avait proposé 400 000 stades, mais je ne sais pas sur la base de quoi…)
Oui, cette méthode est trop compliquée (et il faut attendre un instant à l’intérieur d’une année pour la réaliser…)
Une autre méthode mille fois plus simple et efficace est celle de Al Biruni, savant perse du 10ème siècle
http://www.mathouriste.eu/Al-Biruni/al-biruni.html
En fait, Ératosthène a demandé la distance à différents chameliers, des commerçants, des messagers, et il existait même des arpenteurs professionnels. Il a donc fait une moyenne, ce qui est déjà remarquable comme idée à son époque.
D’ailleurs, si on demande à une centaine de français quelle est la hauteur de la Tour Eiffel et qu’on fait la moyenne des réponses, on trouve la bonne mesure à un mètre près…
Je ne suis pas convaincu par la preuve.
Il se pourrait très bien que la terre soit plate et que le soleil pas si loin que ça de la terre.
À la louche, l’angle mesuré est environ de alpha=2pi/50=.125.
Notons d la distance Alexandrie-Syène et D la distance terre-soleil.
Dans mon hypothèse, on a tan(alpha)=d/D D’où, avec l’approx « quivabien » alpha=tan(alpha), D=d/alpha=40000 stades=6300km.
Cette distance me paraît largement assez grande pour être crédible.
L’explication que j’ai lue quelque part est qu’Eratosthène s’était dit que si la lune et le soleil était rond, il n’y avait pas de raison de penser que la terre était plate. De plus, on peut supposer que c’est l’ombre portée de la terre sur la lune qui cause les phases de la lune et l’observation de ces phases est beaucoup plus compatible avec une terre ronde qu’une terre plate.
Tu as bien raison de ne pas être convaincu par la « preuve », puisque ça n’en est pas une ! Eratosthène ne démontre pas que la Terre est ronde !
Comme je l’ai écrit, il suppose que la Terre est ronde et le Soleil infiniment loin, et sous ces hypothèses se propose d’estimer sa circonférence. Et tu as parfaitement raison, une hypothèse alternative est que la Terre est plate et le Soleil « pas si loin que ça ». On doit même pouvoir forger pour le fun tout un tas d’hypothèses intermédiaires avec une Terre de courbure non-constante 🙂
Dans ces écrits, il justifie que la Terre est ronde par le phénomène de disparition des bateau : en effet, quand les bateaux s’éloignent vers l’horizon, on les voit « disparaître », alors que ce ne serait pas possible avec un disque plat.
Mais je dois avouer que c’est extraordinaire cette méthode pour l’époque, vue par les lycées en seconde (un petit calcul de tangente et hop, le tour est joué)
Eratosthène supposait la Terre sphérique parce que c’était une conviction établie, depuis deux siècles, parmi les philosophes et savants grecs, notamment les Pythagoriciens.
Son calcul a apporté une confirmation supplémentaire que « la Terre est ronde », et une précision remarquable qui servira de base aux discussions jusqu’à l’époque de Christophe Colomb et de Magellan ! Strabon s’en servit, dans l’empire romain, pour expliquer qu’un bateau qui partirait d’Espagne et naviguerait vers l’Ouest atteindrait l’Inde après avoir franchi environ 180.000 stades. Les savants occidentaux ne l’oublieront jamais.
Svp pas de pub pour l’obscurantisme. Surtout de la part d’un vulgarisateur comme toi. Même si l’expérience n’a pas pour objet de démontrer que la terre est ronde parce qu’on le savait déjà 200 ans avant notre aire, le résultat donne une circonférence qui par définition confirme l’hypothèse que la terre est bien ronde selon l’axe nord-sud.
Un premier petit commentaire : l’ombre des phases de la Lune est celle de la Lune elle même, donc la Lune n’est pas un disque mais une sphère. En revanche, lors d’une éclipse de lune, il s’agit cette fois de l’ombre de la terre projetée sur la lune, ombre ronde … La Terre peut être ronde elle aussi.
Un second commentaire : nul besoin d’être sur le même méridien, il suffit de mesurer l’ombre la plus petite, celle du midi local, puis de connaitre la distance séparant les deux parallèles : seulement la partie Nord-Sud.
Pour le second commentaire je suis surpris qu’il n’est pas été mentionné plus tôt.
Je venais pour le rajouter en cas d’absence.
« …De plus, on peut supposer que c’est l’ombre portée de la terre sur la lune qui cause les phases de la lune et l’observation de ces phases est beaucoup plus compatible avec une terre ronde qu’une terre plate. »
Non, les phases n’ont rien à voir avec l’ombre de la terre, mais les éclipses de la lune par la terre oui !
Non car la terre comme on peut le voir sur les images prises de l’espace,est ronde comme toutes les autres planètes …
D’un puits situé sur l’équateur à Sienne(Assouan), et d’un obélisque à Alexandrie à une certaine distance au Nord. Et la mesure de la distance entre Sienne et Alexandrie (mesuré en comptant les pas d’un chameau, selon certains).
Le jours du solstice d’été (21 juin), le soleil passe au zénith du puits à Sienne(latitude 24° environ), comme ses rayons se reflètent sur l’eau au fond du puits on en déduit que, ce jour là, la soleil est bien à la verticale du lieu. 5000 stades plus au nord, à Alexandrie, il a mesuré la longueur de l’ombre de l’obélisque. Connaissant sa hauteur, et la distance entre les 2 villes, une simple raisonnement (niveau 5ieme actuellement) permet de calculer le rayon de la terre en supposant le soleil placé très loin de la terre (donc des rayons parallèles).
Voici quelques liens pour plus de détails:
https://sciencetonnante.wordpress.com/2011/10/03/la-mesure-de-la-circonference-de-la-terre-par-eratosthene/
http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/pratique/textes/eratoste.htm
http://www.math93.com/index.php/histoire-des-maths/les-mathematiciens/liste-complete/184-eratosthene-de-cyrene?start=4
Plus de mille ans après Ératosthène , Al-Biruni , a mesuré le rayon de la terre par une autre méthode. Il mesuré une longueur et des angles, pour déterminer la hauteur du sommet d’une montagne d’où en pouvait voir la mer, puis en mesurant l’angle entre l’horizon (la surface de la mer) et l’horizontale (ou le verticale d’un fil à plomb), il à calculé le rayon de la terre:
http://home.nordnet.fr/~ajuhel/Al-Biruni/al-biruni.html vers le milieu de la page!
Ok dans ce cas explique moi l’éclipse de lune avec ta théorie platiste ? Cela t’est impossible. Par conséquent en appliquant le rasoir dOckham l’hypothèse de la terre ronde est plus simple que l’hypothèse de la terre plate. Comme chacune de ces hypothèse s’excluent et l’hypothèse de la terre plate est plus simple et surtout GLOBALE, EXACTE, et CONFORME aux OBSERVATIONS elle est digne de l’appellation de science contrairement a la théorie (fumeuse) platiste qui n’est ni globale, ni exacte, ni conforme aux observations.
Je voulais bien sur dire que la terre ronde est plus simple et exacte. Désolé pour l’erreur…
bonjour est ce que vous pouvez m’aidez car je dois trouvez la circonférence de la terre en km qui fait 39375 km mais ses pour un devoir maison mais je ne sais pas comment l’expliquer aidez-moi svp
La méthode est décrite dans l’article. Il faut faire la mesure entre le tropique et l’équateur ou entre les tropiques…
Pingback: Anonyme
J’ai reçu d’un excellent ami épris de physique un livre épatant qui raconte la mesure de la grandeur de la terre par Eratosthène. Je viens de terminer la lecture de ce roman attachant de Denis Guedj « Les cheveux de Bérénice » Editions du Seuil. Je vous en recommande la lecture.
Michel R.M.
Je confirme… C’est un livre absolument passionnant racontant jour après jour le voyage à dos de chameau (mulet) des assistants d’Ératosthène qui comptent les pas des animaux toute la journée et font des moyennes le soir à la veillée… On et bien loin des calculs mathématiques et des théorèmes arides…
Pingback: Grimper à l’échelle des distances cosmiques | Science étonnante
Pingback: TPE | Pearltrees
ma parole ken sa rem la societe wesh
on comprend rien a ton message.
de ouf
Ken sa reum les obscurantistes…
Pingback: La mesure de la circonférence de la Terre par Eratosthène | maadi gazette
Pingback: La rotondité de la Terre et les voiles des bateaux | Science étonnante
et depuis on conserve la même méthode ou a t’elle évoluée?
Depuis, on utilise d’autre méthode bien plus précises, Comme la géodésie spatiale, le GPS, et l’interférométrie à grande base.
La précision atteint le mm…
http://renag.unice.fr/regal/PERSO/JMN/enseignement/M2_geodesy_uns/cours_m2_1.pdf
la terre est ronde car le coeficient du caree de la somme prouve par a + b que la terre est ronde . Des satelittes aussi le prouvent surtout les satelites russe .le calcul de la circonference de la terre Erathosthene la casiment trouver a 1650 km pres . A vous de juger cela .
je suis surpris par votre raisonnement selon lequel les deux villes ne sont pas sur le même méridien!!! si j’estime que la terre est une sphère, deux points pris au hazard définissent automatiquement un méridien, de même que deux autres points pris eux aussi au hazard définissent eux aussi un autre un méridien absolument égal au premier même s’il font un angle entre eux et ainsi de suite. Ne faites vous pas un anachronisme avec l’introduction d’un pôle et de méridiens passant strictement par ce pôle?
Je pense que vous confondez avec la notion de « grand cercle ».
Je cite mon encyclopédie préférée :
En géographie, un méridien est un demi cercle imaginaire tracé sur le globe terrestre reliant les pôles géographiques.
A l’époque je doute qu’ils se souciaient du léger écrasement de la terre aux pôles et de l’orthogonalité du méridien entre les deux points.
Et si le calcule d’Eratosthenes était précis ? Ce serait peut-êtrre un preuve que la Terre est en expansion ! (ca 20 cm par an, voir les rifts).
Si la terre est en expansion c’est a cause de l’expansion de la structure de l’univers. Pas de la pression interne de la terre.
sa va
Je n’ai jamais vu de mes yeux un satellite.
13 000 en orbite + des millions de débris. Jamais vu ! Sur aucune photo.
Hormis les schémas et les images de synthèse sur internet, et les prototypes au sol, je ne vois aucune preuve.
Certains me diront qu’ils les voient dans le ciel. Ca reste une loupiote qui clignote. Pourquoi pas un avion en haute ou très haute altitude ?
Même Google utilise des avions pour Google maps.
Pour Eratosthène tout le monde l’aura compris, il part simplement de l’hypothèse que la Terre est ronde. Il n’a rien démontré, mais tout théorisé. Vous le savez, un raisonnement a beau être juste, si l’hypothèse est fausse, alors TOUT est faux.
Lui comme tant d’autres ont théorisé sur du faux si la Terre s’avère plate (Einstein Newton Kepler etc.). Dramatique la taille du mensonge !
Il ne reste plus que l’horizon éventuellement comme matière à discuter…
Selon moi, il n’y a que dans Olive et Tom ou autres films que les objets disparaissent à distance.
On peut voir la Corse en entier depuis Nice (180km) c’est normal ? « Un mirage » diront-ils. De cette qualité, bien sûr !
Ce n’est plus qu’une question de croyance.Dans la Torah la Bible et le Coran, ou alors dans la NASA et les sciences modernes, qui sont justes mais peut-être bâties sur du Faux.
Cher Hugo,
As-tu déjà trouvé par toi-même une pépite d’or, depuis que tu es né ? pourtant tu vois de l’or (alliances, dents en or, dorures, etc.) un peu partout et tu en utilises dans ton téléphone ou dans ton ordinateur tous les jours. Quel argument !
Il suffit de regarder le ciel par une nuit sombre et sans nuage, même pas besoin de lunette, à l’œil nu et tu en verras des satellites… ça file à une vitesse impressionnante, et très régulière. Tu en verras beaucoup plus que des étoiles filantes par exemple. Ah oui, j’oubliais, les étoiles filantes ça n’existe pas de toute façon…
La Terre tourne : le pendule de Foucault est là pour le prouver de manière INCONTESTABLE
https://upload.wikimedia.org/wikipedia/commons/8/82/Foucault-rotz.gif
(ou bien achète un giroscope : tu te verras tourner autour !)
La Terre est ronde, le calcul d’al Biruni est là pour le prouver de manière INCONTESTABLE
https://owlcation.com/stem/How-to-Determin-the-Radius-of-the-Earth-Al-Birunis-Classic-Experiment
Maintenant, il y a une autre certitude universelle : les ânes pensent que la Terre est plate et rien ne pourra les faire changer d’avis, ça c’est aussi incontestable.
Hugo, regarde ces 3 photos de la lune, la 1iere prise dans l’hémisphère nord, la seconde à l’équateur et la dernière dans l’hémisphère sud. Regarde bien les détails de la lune qui changent suivant la latitude de l’observateur. Crois tu pouvoir expliquer cela en partant de l’hypothèse de la terre plate?
Alors qu’avec un globe, c’est simple, la verticale de l’observateur change en fonction de sa latitude, tout simplement…
Oups, j’ai oublié les photos:
https://www.sfrcloud.sfr.fr/web/app/share/invite/21POsY7yRN
Tu veux voir un satellite ? La station spatiale internationale est assez grosse pour être observé a l’oeuil nu quand elle passe après le crépuscules ou avant l’aube. Consulte ton observatoire local et tu les verra de tes propres yeux.
Si la terre est plate explique moi l’éclipse de lune ? Tu peux pas ! Donc la terre est ronde parce que le modèle de la terre ronde est global, exact et conforme aux observations contrairement au modèle de la terre plate.
Google maps utilise des images satellitaires et des Google cars pour streetview pas des avions.
Si t’aime pas les images de la NASA prend celles de l’ESA ou de la Chine ou de la Russie ou de tout autre organisme indépendant qui a pignon sur rue et est reconnu par un état autre que les USA.
La sciences est certes incomplète mais pas fausse contrairement a la religion qui elle peut l’être (pastafarisme). La science peut utiliser des modèles incomplets mais qui restent approchant de la réalité. Une science qui n’approche pas la réalité ou les observations n’est pas une science, c’est de la fumisterie(cf: platisme vs éclipses de lune). La science modélise le monde tel qu’on l’observe. Elle peut être imparfaite et/ou incomplète mais elle ne peut pas être fondamentalement fausse car si on arrive a démontrer qu’elle est fausse elle perd automatiquement son caractère scientifique. Ce qui est faux NE PEUX PAS être scientifique.
Pingback: Islamophobie - oliverstarc | Pearltrees
tout le monde est l’esclave de son patron
Comme tout le monde est l’esclave de sa connerie. La démarche du scientifique est de prouver mathématiquement que sa connerie est fausse. Si il n’y arrive pas pendant un nombre concluant d’expériences il postule que sa connerie peut être vrai tant que personne ne prouve le contraire. La démarche du croyant est de prouver que sa connerie est vrai même si on lui démontre mathématiquement qu’elle est fausse. Et plus on lui démontre qu’elle est fausse mathématiquement plus il se persuade que sa connerie est vrai et juge les autres d’hérétiques. Que voulez vous être, le scientifique ou le croyant ?
Al Biruni, un peu plus tard, a trouvé une méthode beaucoup plus efficace pour calculer le rayon de la Terre :
https://owlcation.com/stem/How-to-Determin-the-Radius-of-the-Earth-Al-Birunis-Classic-Experiment
Merci pour ces explications très claires, c’est très inétressant.
En revanche je serais intéressé par des précisions sur son calcul de l’obliquité de la Terre. C’est l’histoire des angles alternes-internes ? Je précise que je ne suis pas mathématicien…
Pingback: 5ème - SVT Collège | Pearltrees
Pingback: Ressources nouveaux programmes | Pearltrees
par quelles sources connaissons nous Eratosthène et sa méthode géniale ?
La méthode utilisée par Ératosthène est décrite par Cléomède dans sa Théorie circulaire des corps célestes.
voir https://fr.wikipedia.org/wiki/%C3%89ratosth%C3%A8ne
voir les référence en fin de page
Sa ma aider merci
Pingback: Vico12 | Pearltrees
je vois beaucoup de photos des rayons du soleil qui arrivent de façon dispersée en sortant des nuages sur google.à mon humble avis les rayons du soleil ne nous viennent pas parallèle.donc j’ai un gros doute sur tout ça.
Les photos de rayons qui sont « cassés » par la couverture nuageuse ne donnent pas la direction directe soleil-terre, effectivement. Toutefois, Ératosthène faisait ses calculs sur la base de la lumière directe du soleil par temps clair sans nuages.
Al-Biruni a trouvé une méthode plus précise que celle d’Ératosthène pour déterminer la circonférence de la Terre : https://owlcation.com/stem/How-to-Determin-the-Radius-of-the-Earth-Al-Birunis-Classic-Experiment
la lumière que l’on voit passer à travers des nuages ne correspond pas aux rayons du soleil : https://pixabay.com/fr/ciel-nuages-lumi%C3%A8re-du-soleil-1792307/
Cette lumière,ces rayons, des rayons du soleil, mais c’est l’effet de perspective qui nous les fait voir ainsi , en éventail, donc apparemment non parallèles.
Ces pieds de vents, c’est le nom donné pas les Canadiens du Québec aux phénomènes visuels montrant des rayons solaires s »élargissant sous une trouée nuageuse et éclairant plus ou moins ponctuellement la surface de la terre, s’expliquent parfaitement en tenant compte des positions respectives de l’observateur, du soleil et du « trou » dans le nuage, Mais encore faut-il pour visualiser le trajet des rayons lumineux que l’atmosphère diffuse la lumière; donc qu’elle soit un peu chargée en humidité ou en particules.
1- L’observateur, regarde en direction du soleil à travers le « trou » du nuage. Ils n’est pas sous le « trou » nuageux.
2- le soleil n’est pas très « haut » dans le ciel , il est plutôt sur l’avant de l’observateur.
3- La lumière du soleil, passe donc par le « trou » et vient en direction de l’observateur et touche le sol un peu avant. La scène à donc une profondeur que la distance ne permet pas d’appréhender , et les rayons qui donnent l’impression de descendre sous le soleil sont en fait, en général, très inclinés par rapport à la surface de la terre et se dirigent vers l’observateur. En fait :
– S’ils descendent verticalement, leurs trajectoire est perpendiculaire au sol.
– S’ils forment un « éventail » presque fermé, ils se rapprochent de l’observateur
– Plus l’éventail est ouvert et plus ils se rapprochent.*
Pour visualiser comment cet éventail apparent se forme, imaginez vous tout petit, un peu en hauteur et au milieu d’un voie ferrée. Si l’on compare les deux rails aux rayons parallèles du soleil, essayer de vous représenter ce que vous verriez!
Au loin devant vous les 2 rails sont confondus, c’est le Soleil. Ses 2 rayons(les rails) s’écartent l’un de l’autre lorsque vous regardez plus près. Et si vous êtes tout petit, vous verrez les deux rails s’écarter de plus en plus, suivant votre hauteur.
En étant placé entre les rails, vous verrez même les rails s’écarter de 180°.
Et bien c’est la même chose pour les « pieds de vent », les rayons, rendus visibles par les particules de l’atmosphère « s’évasent » tout simplement par un effet de perspective. Et plus ils s’approchent de l’observateur plus ils semblent s’écarter…
En fait , ils suffit de voir la scène en 3D, et les constructions géométriques 2D, réalisées sur les photos n’indiquent que la position du soleil sur la photo, sa hauteur angulaire éventuellement sur l’horizon, mais absolument par sa distance.
Ce genre de rayon en éventail, s’observe aussi en forêt les jours de brouillard léger et cela démontre bien qu’il est ridicule de vouloir mesurer la hauteur du soleil par ce procédé (il serait alors de quelques dizaines de mètre maximum)…
D’abord l’atmosphère fait lentille ensuite quand tu ferme une porte d’une pièce éclairé dans un couloir sombre une partie de la lumière se disperse dans des axes qui ne correspondent pas a la droite lampe-fente. C’est l’expérience des fentes de young. La lumière se propage selon une onde de propagation. A travers les nuages les trous se comportent comme les fentes de young dispersant la lumière dans des axes qui ne correspondent pas a l’axe soleil-trous-de-nuages. De plus l’eau contenue dans le nuage environnant augmente cet effet en diffractant la lumière.
Et pourquoi ne pas faire vos expériences et mesurer le rayon de la terre, sans aller à l’équateur, chez vous et seulement:
» – Un chronomètre
– Un manche à balai marqué de deux repères: B près de son œil quand on est debout, le manche à balai étant posé verticalement. Et A, près du sol, accessible quand on est accroupi ou couché… »
Voir :
http://l.facebook.com/l.php?u=http%3A%2F%2Fphilippe.boeuf.pagesperso-orange.fr%2Frobert%2Fastronomie%2Frayonterre.htm&h=EAQFoOpyg
la terre et plate bande de con toute les photo de la nasa son truquer
Très intéressante cette phrase, mais pourriez-vous être plus explicite???
Moi je remarque que les détails visibles de la surface de de la lune changent d’orientation angulaire, lorsque je change de latitude. Et, chose incroyable, et inexplicable sur une terre plate, que le changement d’angle correspond pile-poil à celui de mon changement de latitude.
Comment expliquez vous cela Monsieur Boula??? 😀
Une remarque pertinente?
Plus simple demande lui d’expliquer les éclipses de lune. Avec une terre plate c’est impossible… Parce que la terre ne passe jamais entre la lune et le soleil dans un modèle platiste…
La terre est ronde c’est ton encéphalogramme qui est plat… J’ai pas besoins des photo de la NASA pour calculer le rayon de la terre avec la méthode d’Ératosthène…
Et si il y à rayon c’est forcément qu’elle est ronde…
svp de quoi c’est servi Eratosthéne pour réalise ces expériences
D’un puits situé sur l’équateur à Sienne(Assouan), et d’un obélisque à Alexandrie à une certaine distance au Nord. Et la mesure de la distance entre Sienne et Alexandrie (mesuré en comptant les pas d’un chameau, selon certains).
Le jours du solstice d’été (21 juin), le soleil passe au zénith du puits à Sienne(latitude 24° environ), comme ses rayons se reflètent sur l’eau au fond du puits on en déduit que, ce jour là, la soleil est bien à la verticale du lieu. 5000 stades plus au nord, à Alexandrie, il a mesuré la longueur de l’ombre de l’obélisque. Connaissant sa hauteur, et la distance entre les 2 villes, une simple raisonnement (niveau 5ieme actuellement) permet de calculer le rayon de la terre en supposant le soleil placé très loin de la terre (donc des rayons parallèles).
Voici quelques liens pour plus de détails:
https://sciencetonnante.wordpress.com/2011/10/03/la-mesure-de-la-circonference-de-la-terre-par-eratosthene/
http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/pratique/textes/eratoste.htm
http://www.math93.com/index.php/histoire-des-maths/les-mathematiciens/liste-complete/184-eratosthene-de-cyrene?start=4
Plus de mille ans après Ératosthène , Al-Biruni , a mesuré le rayon de la terre par une autre méthode. Il mesuré une longueur et des angles, pour déterminer la hauteur du sommet d’une montagne d’où en pouvait voir la mer, puis en mesurant l’angle entre l’horizon (la surface de la mer) et l’horizontale (ou le verticale d’un fil à plomb), il à calculé le rayon de la terre:
http://home.nordnet.fr/~ajuhel/Al-Biruni/al-biruni.html vers le milieu de la page!
Syène (Assouan) n’est pas située sur l’équateur mais sur le tropique du Cancer qui est dans l’hémisphère nord à latitude 23° 26′ 13.490″ , c’est-à-dire à environ 2930 km au nord de l’équateur.
Un puis (avec de l’eau) et un bâton ou une construction réputé localement à 90° du sol. Après tout est de la trigo de base.
On peux faire pareil avec deux bâtons a 90° suffisamment éloignés pour pouvoir mesurer un écart de longueur d’ombres entre les 2 bâtons. Le mieux étant qu’ils soient sur le même méridien.
Pingback: Pythagore Vs Aristote – L'atterrement
Merci pour cet excellent article et plus généralement pour la qualité de votre travail de vulgarisation et de pédagogie.
Il y a juste une chose que je ne trouvais pas hyper claire en première lecture : comment Eratosthène a-t-il fait pour synchroniser ses deux mesures ? Que veut dire midi pile le 21 juin à Alexandrie à une époque où l’on n’a pas de montre ?
En formulant cette question, il m’arrive ce qui arrive souvent à mes élèves : j’y réponds soudain moi-même. Efficacité de la dialectique. J’imagine que c’est le moment où l’ombre est la plus courte. C’est tout con, mais les articles sur le sujet gagneraient à le préciser, je pense.
C’est le midi solaire, donc l’ombre la plus courte évidemment!
Je me suis également souvent demandé comment on synchronisait les deux mesures !
Et cette réponse n’est qu’à motié satifaisante, parcequ’a prirori on ne peut savoir qu’après coup l’instant où l’ombre était la plus courte ?
On se repérait peut êre sur la position de l’ombre la plus courte de la veille.
Mais comment faire pour que ce ne soit pas à peu près, c’est à dire au pif ?
On procède à toute une série de mesures, aux alentours du point estimé ?
et on retient celle qui correspond le mieux après coup ?
<>
La réponse est simple, il suffit de marquer l’extrémité de l’ombre à intervalle de temps régulier … 😀
Très bon article , explicable pour les 5e qui ont cours dessus , ça m’évite de trop réfléchir 5 minutes pour rien 🙂
Le but de l’apprentissage c’est d’apprendre a réfléchir convenablement … Trouver une solution a un problème est bien plus gratifiant qu’obtenir la solution toute cuite dans le bec et est bien plus profitable car on se souviendra du cheminement de pensée pour l’obtenir…
Pingback: Les maths, c'est la vie? - Blog NSellier TV
Pingback: De la Terre à la Lune – Automaths
avis au amateur de la terre plate soit des illuminés ératosthene a fait ces calculs suivant pole nord pole sud pour trouver environ 40 000 km hors si l on calcule la circonférence a l équateur on trouve environ la méme chose . normal la terre est une sphére aplatie légerement aux poles faitent unerepresentaion de ces deux calcul . EN TRACANT DEUX CERLES ;UN SUR L 2QUATEUR AUTRE EN PASSANT PAR LES POLES BREF a l impossile nul imbécile est tenu de le faire
Pingback: La Terre est ronde et c'est un jeu d'enfant de le prouver - MEDIAVOR
Pingback: La Terre est ronde et c’est un jeu d’enfant de le prouver | Nuage Ciel d'Azur
Il n y a personne qui a vu le « mis » dans le paragraphe le soleil au fond des puits a « il a miS » il devrait y avoir un « t » a la place .
Tiens je savais pas que capelovici était ressuscité…
Bonjour,
Je ne suis pas d’accord avec une des hypothèses présentées, il n’a absolument pas besoin que les villes de syène et d’alexandrie soient sur le même méridien. Pour la simple raison que le soleil était au zénith, de ce fait, le baton de syène, celui d’alexandrie et l’ombre à alexandrie sont coplanaires (sous entendu par la proposition des deux autres) le résultat obtenu donnera la circonférence de la terre par un cercle ne passant pas par les deux poles, mais l’hypothèse de dire que la terre est ronde règle alors le problème.
Bien cordialement
Anthony
Sauf que pour faire le calcul , il faut la distance entre les deux latitudes suivant un méridien…
C’est presque le cas pour Syène et Alexandrie….
une nouvelle fois, il assimile la terre à une sphere, cette propriété implique que alexandrie et syene soit sur un meme méridien.
par ailleurs, les rayons du soleil sont considéré parallèle, comme il prend la mesure au niveau de l’équateur, à cet instant, la position de l’ombre à alexandrie en longueur est la meme que celle se trouvant sur le meme meridien (au sens passant par les poles) de syene avec la distance alexandrie-syene
La mesure a été refaite simultanément par des écoles, en plusieurs endroits, et , sans faire d’hypothèse sur la forme à priori, le seul modèle qui colle aux mesures est la sphère…
Vous pouvez aussi mesurer la direction et la hauteur du soleil en de nombreux lieux sur terre, et représenter ces directions (et les distances entre lieux) dans une représentation 3D animée, passant d’un plan (sphère de rayon infini) à la sphère terrestre.
Le seul endroit les tracés pointent vers le même point (le soleil) est lorsque le rayon est proche de 6378km….
Bonjour !
J’ai trouvé votre explication très intéressante mais j’ai une question : Comment Eratosthène a-t-il pu mesurer les angles d’arrivée des rayons du soleil le même jour à deux endroits très éloignés l’un de l’autre ? Aurait-il fait ses mesures à 1 an d’intervalle ? Est-ce qu’au bout d’1 an et le même jour, le soleil était à la même place que l’année d’avant ?
Merci
Simple, Il sait que tous les ans aux solstices, le soleil se reflète au fond du puits. Donc ces jours là, le soleil est perpendiculaire à l’horizontal du lieu Il lui suffisait donc de connaitre la hauteur de l’obélisque, la longueur de l’ombre et la distance Alexandrie-Syène pour calculer le rayon de la terre…
https://www.intellego.fr/soutien-scolaire-2nde/aide-scolaire-physique/mesure-du-rayon-de-la-terre-par-la-methode-d-eratosthene./26823
Merci beaucoup ! 🙂
Oui ça a été mesuré a un an d’intervalle sur les 2 points au solstice. En s’étant assuré que durant plusieurs solstice d’été le soleil eclairait pleinement le fond d’un puis. Du coups il n’y avait pas de raisons que le solstice suivant le phénomène change.
woaw c beau
merci beaucoup
Pingback: H5- L'essor des sciences en Europe aux XVII-XVIIIe siècles | Pearltrees
Pingback: Histoire des Sciences | Pearltrees
Pingback: Eratosthène:Terre est ronde, calcul de sa circonférence avec la géométrie de 5ème! | Pearltrees
Pingback: Mesure de la circonférence de la Terre | Pearltrees
slt! , Ératosthène c’est intéressante la choses
Bonjour!
Je fais justement un article sur le sujet dans lequel je m’amuse à mettre en application l’expérience d’Ératosthène pour voir le résultat que ça donne quand on fait l’expérience nous même. ça donne des résultats très intéressant. Je laisse le lien pour ceux que ça intéresse de voir ce que ça donne de réaliser l’expérience ainsi que de donner à ceux qui le souhaite les outils pour le faire aussi eux même 🙂
https://www.facebook.com/ZimExp/
Je remet en cause cette réponse étant donné que syène ne se situe pas sur le même méridien que Alexandrie et par ailleurs le parcours à dos de chameau ne sera pas exact compte tenu de la fatigue de l’animal et de la mauvaise état de route.
L’expérience a été répliquée plusieurs fois depuis, et surtout le même jour à divers endroits les jours d’équinoxes. Les mesures sont conformes et indiquent bien la taille de la terre et que le soleil est bien à l’infini.
Beaucoup de mesures de distance ont été réalisées en comptant des pas, d’animaux ou de personnes entraînées.
En 1800, il y avait encore , en France, des personnes chargées de relever des cartes dans certains pays d’Afrique, qui suivaient un entrainement spécial pour apprendre marcher d’un pas de longueur fixe et connue. Car sortir un instrument scientifique aurait été dangereux pour leur sécurité…
Le chameau est réputé pour avoir un pas régulier, est de nombreuse expérience et mesure de distance ont été réalisée grâce à eux. La fatigue n’est pas un problème, la caravane s’arrêtant tous les soirs, et que savez-vous de l’état de la route?
Mettre un lacet de longueur connue entre les chaussures suffit a garantir la mesure pas besoins d’outils complexes. La chaine d’arpenteur vous connaissez ?
L’erreur de mesure se retrouve dans l’erreur de résultat…
Pingback: SAVIEZ-VOUS QUE : 200 ANS AV. J-C, ÉRATOSTHÈNE SE TROMPAIT DE 700 KM EN CALCULANT LA CIRCONFÉRENCE DE LA TERRE
Pingback: Eratosthène (-200): réussit à calculer la circonférence de la Terre: | Pearltrees
Pingback: L'avion a changé la notion de voyage | CATPW
bin moi, je suis né à Nancy, et ma maman dit toujours que je suis son soleil! Alors oui il y a un soleil à Nancy. CQFD.
Pingback: Circonférence | Pearltrees
Comment l’Education Nationale Laique peut-elle tollérer qu’il y ait encore en France, pays des « Lumières » des écoliers qui affirment que la terre est plate ? Il faut faire comprendre aux jeunes musulmans que les données de la science s’imposent par la connaissance, basée sur l’expérience et la raison sur les croyances religieuses ou idéologiques. Ce furent les premiers chrétiens qui ont répandu l’idée que la terre est plate « pasque sét écri da la bibe »: dans leur haine pour les payens, adorateurs de faux dieux, ils ont rejetté même les enseignements des sciences des Mésopotamiens, Egyptiens, Grecs, Latins, Chinois, tous adorateur de faux dieux. Malgré le cri d’allarme de St Augustin qui invitait les chrétiens à ne pas se faire passer pour des crétins aux yeux des contemporains en rejettant l’évidence, l’Eglise catholique a beaucoup peiné à suivre son conseil et même aujour’hui elle hésite à décanoniser l’Ancien Testament, qui est un ensemble de textes religieux juifs étrangers voir contraires au catholicisme. Suivant l’hérésie de Luther, le fondateur du protestantisme, pour lequel la Sainte Bible contient la parole même de Dieu et est par conséquent l’unique source de la vérité, certaines sectes protestantes continuent à affirmer aujourd’hui encore que la terre est plate (God says it in the Holy Bible) .L’Américain William Carpenter a publié en 1860 « Cent preuves que la terre est plate » et Boula & co peuvent aujour’hui, si ça leur chante, s’incrire à la US Flat Earth Society
qui affirme que le mythe de la terre sphérique est soutenu par une conjuration mondiale qui répand de fausses croyances pour égarer les vrais chrétiens !
L’église n’a jamais affirmé que la terre est plate, la sphéricité de la terre est démontrée depuis bien trop longtemps et avec beaucoup trop d’évidence pour que l’église aille contre ce fait. Cependant, l’église ne reconnu pas l’heliocentrisme quand ce fait fut découvert.
Aujourd’hui, seuls quelques crétins se revendiquant du christianisme ou encore de l’islam ne reconnaîssent pas la sphéricité de la planète.
Pingback: La mesure de la circonférence de la Terre par Eratosthène | Pearltrees
Salut à tous,
Quelqu’un peut m’expliquer comment connaître le méridien de sa ville ?
Merci 🙂
Pour avoir le méridien géographique du lieu,
lancer GoogleEarth https://earth.google.com/web/
Cherchez le lieu en question, placez le curseur sur l’emplacement du lieu recherché et regardez en bas à droite:
– le premier chiffre est l’altitude de l’observateur en km
– le second, la latitude en ° ‘ » Nord ou Sud (°= degré, ‘=minute et « =seconde)
– le troisième la Longitude, encore appelée Méridien du lieu. en ° ‘ » Ouest/Est (°= degré, ‘=minute et « =seconde)
Pingback: Quelle est la Taille de la Terre ? #03 Science - Qualitay.fr
Pingback: Eduscol et Lamap | Pearltrees
Pingback: Est-ce raisonnable de faire confiance aux scientifiques ?
Pingback: OVNIs ? – Maïté Molla Petot
Juste pour info, Ô dieu de la vulgarisation, un site au produits saugrenus (du lait de chameau) a copié cet article pour le publier sur son propre site. peut-être est-ce normal mais dans le doute voilà un lien : https://camel-idee.com/mesure-de-la-circonference-avec-un-chameau/ .